Boundary value problems exercise solutions#
Solutions to the exercises on boundary value problems.
Solution to Exercise 5.1
(a) \(p(t) = -\dfrac{4}{t}\), \(q(t) = \dfrac{2}{t^2}\) and \(r(t) = \dfrac{2\ln(t)}{t^3}\) are all continuous and \(q(t) > 0\) for \(t \in [1, 2]\) so this boundary value problem has a unique solution.
(b) \(p(t) = -(t + 1)\), \(q(t) = \cos(t)\) and \(r(t) = e^t\) are all continuous for \(t\in[0,2]\) but \(q(t) < 0\) for \(t \in (\pi/2, 2]\) so this boundary value problem does not have a unique solution.
(c) \(p(t) = 0\), \(q(t) = t^3 + 5\) and \(r(t) = \sin(t)\) are all continuous and \(q(t) > 0\) for \(t\in[0,1]\) so this boundary value problem has a unique solution.
(d) \(p(t) = 0\), \(q(t) = 5e^t\) and \(r(t) = e^t\sin(3t)\) are all continuous and \(q(t) > 0\) for \(t\in[0,1]\) so this boundary value problem has a unique solution.
Solution to Exercise 5.2
Rewriting the ODE as a system of two first-order ODEs
\[\begin{align*}
y_1' &= y_2, \\
y_2' &= 2t.
\end{align*}\]
Solving using the Euler method and \(y'(0)=1\)
\[\begin{align*}
\vec{y}_0 &= (1.000000, 1.000000), \\
t_{0} &= 0.0, \\ \\
\vec{y}_1 &= \vec{y}_0 + h\vec{f}(t_0, \vec{y}_0) \\
&= (1.000000, 1.000000) + 0.4(1.000000, 2(0.0)) \\
&= (1.400000, 1.000000), \\
t_{1} &= t_{0} + h = 0.0 + 0.4 = 0.4, \\ \\
\vec{y}_2 &= \vec{y}_1 + h\vec{f}(t_1, \vec{y}_1) \\
&= (1.400000, 1.000000) + 0.4(1.400000, 2(0.4)) \\
&= (1.800000, 1.320000), \\
t_{2} &= t_{1} + h = 0.4 + 0.4 = 0.8, \\ \\
\vec{y}_3 &= \vec{y}_2 + h\vec{f}(t_2, \vec{y}_2) \\
&= (1.800000, 1.320000) + 0.4(1.800000, 2(0.8)) \\
&= (2.328000, 1.960000), \\
t_{3} &= t_{2} + h = 0.8 + 0.4 = 1.2, \\ \\
\vec{y}_4 &= \vec{y}_3 + h\vec{f}(t_3, \vec{y}_3) \\
&= (2.328000, 1.960000) + 0.4(2.328000, 2(1.2)) \\
&= (3.112000, 2.920000), \\
t_{4} &= t_{3} + h = 1.2 + 0.4 = 1.6, \\ \\
\vec{y}_5 &= \vec{y}_4 + h\vec{f}(t_4, \vec{y}_4) \\
&= (3.112000, 2.920000) + 0.4(3.112000, 2(1.6)) \\
&= (4.280000, 4.200000), \\
t_{5} &= t_{4} + h = 1.6 + 0.4 = 2.0.
\end{align*}\]
Solving using \(y'(0)=-1\)
\[\begin{align*}
\vec{y}_0 &= (1.000000, -1.000000), \\
t_{0} &= 0.0, \\ \\
\vec{y}_1 &= \vec{y}_0 + h\vec{f}(t_0, \vec{y}_0) \\
&= (1.000000, -1.000000) + 0.4(1.000000, 2(0.0)) \\
&= (0.600000, -1.000000), \\
t_{1} &= t_{0} + h = 0.0 + 0.4 = 0.4, \\ \\
\vec{y}_2 &= \vec{y}_1 + h\vec{f}(t_1, \vec{y}_1) \\
&= (0.600000, -1.000000) + 0.4(0.600000, 2(0.4)) \\
&= (0.200000, -0.680000), \\
t_{2} &= t_{1} + h = 0.4 + 0.4 = 0.8, \\ \\
\vec{y}_3 &= \vec{y}_2 + h\vec{f}(t_2, \vec{y}_2) \\
&= (0.200000, -0.680000) + 0.4(0.200000, 2(0.8)) \\
&= (-0.072000, -0.040000), \\
t_{3} &= t_{2} + h = 0.8 + 0.4 = 1.2, \\ \\
\vec{y}_4 &= \vec{y}_3 + h\vec{f}(t_3, \vec{y}_3) \\
&= (-0.072000, -0.040000) + 0.4(-0.072000, 2(1.2)) \\
&= (-0.088000, 0.920000), \\
t_{4} &= t_{3} + h = 1.2 + 0.4 = 1.6, \\ \\
\vec{y}_5 &= \vec{y}_4 + h\vec{f}(t_4, \vec{y}_4) \\
&= (-0.088000, 0.920000) + 0.4(-0.088000, 2(1.6)) \\
&= (0.280000, 2.200000), \\
t_{5} &= t_{4} + h = 1.6 + 0.4 = 2.0, \\ \\
\end{align*}\]
Solution to Exercise 5.3
Calculate the improved guess value
\[\begin{align*}
s_2 &= s_1 + g(s_1) \frac{s_1 - s_0}{g(s_1) - g(s_0)} \\
&= -1 + (3 - 0.28) \frac{1 - (-1)}{(3 - 0.28) - (3 - 4.28)} \\
&= 0.36
\end{align*}\]
Solving using the Euler method with \(y'(0) = 0.36\)
\[\begin{align*}
\vec{y}_0 &= (1.000000, 0.360000), \\
t_{0} &= 0.0, \\ \\
\vec{y}_1 &= \vec{y}_0 + h\vec{f}(t_0, \vec{y}_0) \\
&= (1.000000, 0.360000) + 0.4(1.000000, 2(0.0)) \\
&= (1.144000, 0.360000), \\
t_{1} &= t_{0} + h = 0.0 + 0.4 = 0.4, \\ \\
\vec{y}_2 &= \vec{y}_1 + h\vec{f}(t_1, \vec{y}_1) \\
&= (1.144000, 0.360000) + 0.4(1.144000, 2(0.4)) \\
&= (1.288000, 0.680000), \\
t_{2} &= t_{1} + h = 0.4 + 0.4 = 0.8, \\ \\
\vec{y}_3 &= \vec{y}_2 + h\vec{f}(t_2, \vec{y}_2) \\
&= (1.288000, 0.680000) + 0.4(1.288000, 2(0.8)) \\
&= (1.560000, 1.320000), \\
t_{3} &= t_{2} + h = 0.8 + 0.4 = 1.2, \\ \\
\vec{y}_4 &= \vec{y}_3 + h\vec{f}(t_3, \vec{y}_3) \\
&= (1.560000, 1.320000) + 0.4(1.560000, 2(1.2)) \\
&= (2.088000, 2.280000), \\
t_{4} &= t_{3} + h = 1.2 + 0.4 = 1.6, \\ \\
\vec{y}_5 &= \vec{y}_4 + h\vec{f}(t_4, \vec{y}_4) \\
&= (2.088000, 2.280000) + 0.4(2.088000, 2(1.6)) \\
&= (3.000000, 3.560000), \\
t_{5} &= t_{4} + h = 1.6 + 0.4 = 2.0, \\ \\
\end{align*}\]
The solutions to this boundary value problem using the Euler method with the shooting method are tabulated below.
\(t\) |
\(y_1\) |
\(y_2\) |
|---|---|---|
0.0 |
1.000000 |
0.360000 |
0.4 |
1.144000 |
0.360000 |
0.8 |
1.288000 |
0.680000 |
1.2 |
1.560000 |
1.320000 |
1.6 |
2.088000 |
2.280000 |
2.0 |
3.000000 |
3.560000 |
Solution to Exercise 5.4
\[\begin{align*}
y'' &= 2t, \\
\frac{y_{i-1} - 2 y_i + y_{i+1}}{h^2} &= 2 t_i \\
y_{i-1} - 2y_i + y_{i+1} &= 2 h^2 t_i
\end{align*}\]
which can be written as the matrix equation
\[\begin{align*}
\begin{pmatrix}
1 & 0 \\
1 & -2 & 1 \\
& \ddots & \ddots & \ddots \\
& & 1 & -2 & 1 \\
& & & 0 & 1
\end{pmatrix}
\begin{pmatrix} y_0 \\ y_1 \\ \vdots \\ y_{n-1} \\ y_{n} \end{pmatrix} =
\begin{pmatrix} 1 \\ 2 h^2 t_1 \\ \vdots \\ 2 h^2 t_{n-1} \\ 3 \end{pmatrix}
\end{align*}\]
Since \(h=0.4\) then \(\vec{t} = (0, 0.4, 0.8, 1.2, 1.6, 2)\) and
\[\begin{align*}
\begin{pmatrix}
1 & 0 \\
1 & -2 & 1 \\
& 1 & -2 & 1 \\
& & 1 & -2 & 1 \\
& & & 1 & -2 & 1 \\
& & & & 0 & 1
\end{pmatrix}
\begin{pmatrix} y_0 \\ y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \end{pmatrix} =
\begin{pmatrix} 1 \\ 0.128 \\ 0.256 \\ 0.384 \\ 0.512 \\ 3 \end{pmatrix}
\end{align*}\]
Performing the forward sweep of the Thomas algorithm
\[\begin{align*}
b_1 &= 1, \\
b_2 &= b_2 - c_1 \left( \frac{a_2}{b_1} \right) = -2 - 0\left( \frac{1}{1} \right) = -2, \\
b_3 &= b_3 - c_2 \left( \frac{a_3}{b_2} \right) = -2 - \left( \frac{1}{-2} \right) = -1.5, \\
b_4 &= b_4 - c_3 \left( \frac{a_4}{b_3} \right) = -2 - \left( \frac{1}{-1.5} \right) = -1.333333, \\
b_5 &= b_5 - c_4 \left( \frac{a_5}{b_4} \right) = -2 - \left( \frac{1}{-1.333333} \right) = -1.25, \\
b_6 &= b_6 - c_5 \left( \frac{a_6}{b_5} \right) = 1 - \left( \frac{0}{-1.25} \right) = 1, \\
d_1 &= 1, \\
d_2 &= d_2 - d_1 \left( \frac{a_2}{b_1} \right) = 0.128 - 1 \left( \frac{1}{1} \right) = -0.872, \\
d_3 &= d_3 - d_2 \left( \frac{a_3}{b_2} \right) = 0.256 - (-0.872) \left( \frac{1}{-2} \right) = -0.18, \\
d_4 &= d_4 - d_3 \left( \frac{a_4}{b_3} \right) = 0.384 - (-0.18) \left( \frac{1}{-1.5} \right) = 0.264, \\
d_5 &= d_5 - d_4 \left( \frac{a_5}{b_4} \right) = 0.512 - (0.264) \left( \frac{1}{-1.333333} \right) = 0.71, \\
d_6 &= d_6 - d_5 \left( \frac{a_6}{b_5} \right) = 3 - (0.71) \left( \frac{0}{-1.25} \right) = 3, \\
\end{align*}\]
Performing the back substitution step
\[\begin{align*}
y_6 &= \frac{d_6}{b_6} = \frac{3}{1} = 3, \\
y_5 &= \frac{d_5 - c_5 y_6}{b_5} = \frac{0.71 - 3}{-1.25} = 1.832, \\
y_4 &= \frac{d_4 - c_4 y_5}{b_4} = \frac{0.264 - 1.832}{-1.333333} = 1.176, \\
y_3 &= \frac{d_3 - c_3 y_4}{b_3} = \frac{-0.18 - 1.176}{-1.5} = 0.904, \\
y_2 &= \frac{d_2 - c_2 y_3}{b_2} = \frac{0.872 - 0.904}{-2} = 0.888, \\
y_1 &= \frac{d_1 - c_1 y_2}{b_1} = \frac{1 - 0(0.205992)}{1} = 1, \\
\end{align*}\]
The solutions to this boundary value problem using the finite-difference method are tabulated below.
\(t\) |
\(y\) |
|---|---|
0.00 |
0.0000 |
0.40 |
0.8880 |
0.80 |
0.9040 |
1.20 |
0.1760 |
1.60 |
1.8320 |
2.00 |
3.0000 |
Solution to Exercise 5.5
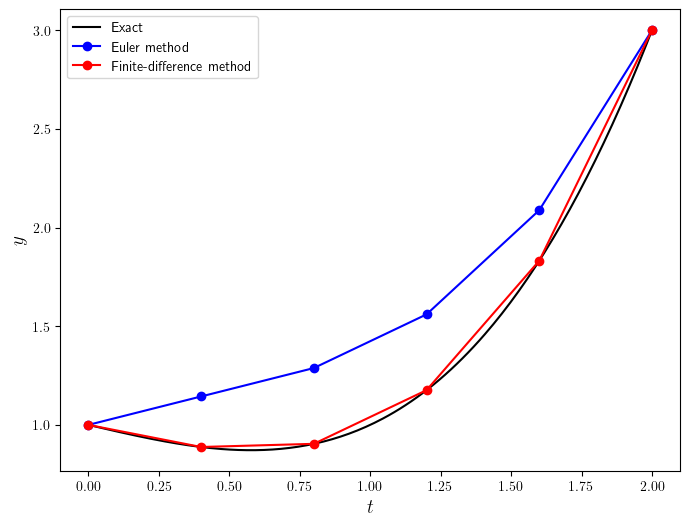
The finite-difference method gives significantly more accurate solutions than the Euler method. This is because the finite-difference used a second-order approximation whereas the Euler method is only first-order. We would expect a more accurate method such as the RK4 method to give similar solutions to the finite-difference method.
Code
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['text.usetex'] = True # allows use of LaTeX in labels
# Define Euler method
def euler(f, tspan, y0, h):
# Initialise t and y arrays
t = np.empty(100000)
y = np.empty((100000,len(y0)))
t[0] = tspan[0]
y[0,:] = y0
# Loop through steps
n = 0
while t[n] < tspan[1]:
# Ensure t does not exceed tspan[1]
h = min(h, tspan[1] - t[n])
# Calculate Euler method
y[n+1,:] = y[n,:] + h * f(t[n], y[n,:])
t[n+1] = t[n] + h
n += 1
return t[:n+1], y[:n+1,:]
# Define shooting method
def shooting_method(solver, f, tspan, bvals, h, tol=1e-6):
s, sprev, gprev = 1, 2, 1
for _ in range(10):
t, y = solver(f, tspan, [bvals[0], s], h)
g = bvals[1] - y[-1,0]
s, sprev, gprev = s - g * (s - sprev) / (g - gprev), s, g
if abs(s - sprev) < tol:
break
return t, y
# Define tri-diagonal solver
def tridiagonal_solver(a, b, c, d):
n = len(b)
for i in range(1, n):
w = a[i] / b[i-1]
b[i] -= w * c[i-1]
d[i] -= w * d[i-1]
x = np.zeros(n)
x[-1] = d[-1] / b[-1]
for i in range(n - 2, -1, -1):
x[i] = (d[i] - c[i] * x[i+1]) / b[i]
return x
# Define ODE functions
def f(t, y):
return np.array([y[1], 2 * t])
def exact(t):
return 1 / 3 * t ** 3 - 1 / 3 * t + 1
# Define BVP parameters
tspan = [0, 2] # boundaries of the t domain
bvals = [1, 3] # boundary values
h = 0.4 # step length
svals = [1, -1]
# Solve BVP using the shooting method
t, y_euler = shooting_method(euler, f, tspan, bvals, h)
# Solve BVP using the finite-difference method
n = int((tspan[1] - tspan[0]) / h) + 1
t = np.arange(n) * h
a, b, c, d = [np.zeros(n) for _ in range(4)]
b[::n-1] = 1
d[::n-1] = bvals
for i in range(1, n - 1):
a[i] = 1
b[i] = -2
c[i] = 1
d[i] = 2 * h ** 2 * t[i]
y_fdm = tridiagonal_solver(a, b, c, d)
# Calculate exact solution
t_exact = np.linspace(tspan[0], tspan[1], 200)
y_exact = exact(t_exact)
# Plot solutions
fig, ax = plt.subplots(figsize=(8, 6))
plt.plot(t_exact, y_exact, "k", label="Exact")
plt.plot(t, y_euler[:,0], "bo-", label="Euler method")
plt.plot(t, y_fdm, "ro-", label="Finite-difference method")
plt.xlabel("$t$", fontsize=14)
plt.ylabel("$y$", fontsize=14)
plt.legend()
plt.show()
% Define ODE
f = @(t, y) [y(2), 2 * t];
% Define exact solution
exact = @(t) 1 / 3 * t .^ 3 - 1 / 3 * t + 1;
% Define BVP
tspan = [0, 2];
bvals = [1, 3];
h = 0.4;
% Solve BVP using the shooting method
[t, y_euler] = shooting_method(@euler, f, tspan, bvals, h, 1e-4);
% Solve BVP using finite-difference method
n = floor((tspan(2) - tspan(1)) / h) + 1;
t = (0 : n - 1) * h;
a = zeros(n, 1);
b = zeros(n, 1);
c = zeros(n, 1);
d = zeros(n, 1);
b([1, end]) = 1;
d([1, end]) = bvals;
for i = 2 : n - 1
a(i) = 1;
b(i) = -2;
c(i) = 1;
d(i) = 2 * h ^ 2 * t(i);
end
y_fdm = tridiagonal_solver(a, b, c, d);
% Calculate exact solution
t_exact = linspace(tspan(1), tspan(2), 200);
y_exact = exact(t_exact);
% Plot solutions
plot(t_exact, y_exact, "k", LineWidth=2)
hold on
plot(t, y_euler(:, 1), "b-o", LineWidth=2, MarkerFaceColor="b")
plot(t, y_fdm, "r-o", LineWidth=2, MarkerFaceColor="r")
hold off
axis padded
xlabel("$t$", FontSize=14, Interpreter="latex")
ylabel("$y$", FontSize=14, Interpreter="latex")
legend("Exact", "Euler method", "Finite-difference method", Location="northwest")
%% ----------------------------------------------------------------------------
function [t, y] = euler(f, tspan, y0, h)
nsteps = floor((tspan(2) - tspan(1)) / h);
neq = length(y0);
t = (0 : nsteps) * h;
y = zeros(nsteps + 1, neq);
y(1, :) = y0;
for n = 1 : nsteps
y(n+1, :) = y(n, :) + h * f(t(n), y(n, :));
end
end
%% ----------------------------------------------------------------------------
function [t, y] = shooting_method(solver, f, tspan, bvals, h, tol)
s = 1;
so = 2;
go = 1;
for i = 1 : 10
[t, y] = solver(f, tspan, [bvals(1), s], h);
g = bvals(2) - y(end,1);
temp = s;
s = s - g * (s - so) / (g - go);
so = temp;
go = g;
if abs(s - so) < tol
break
end
end
end
%% ----------------------------------------------------------------------------
function x = tridiagonal_solver(a, b, c, d)
n = length(b);
for i = 2 : n
w = a(i) / b(i-1);
b(i) = b(i) - w * c(i-1);
d(i) = d(i) - w * d(i-1);
end
x = zeros(n, 1);
x(n) = d(n) / b(n);
for i = n - 1 : -1 : 1
x(i) = (d(i) - c(i) * x(i+1)) / b(i);
end
end