5.4. Boundary value problems exercises#
Answer the following exercises based on the content from this chapter. The solutions can be found in the appendices.
Exercise 5.1
Determine which of the following BVPs have a unique solution
(a) \(y'' = - \dfrac{4}{t} y' + \dfrac{2}{t^2 } y - \dfrac{2\ln (t)}{t^3 }, \qquad y(1) = \frac{1}{2}, \qquad y(2) = \ln (2)\);
(b) \(y'' = e^t + y\cos(t) - (t + 1) y', \qquad y(0) = 1, \qquad y(2) = \ln(3)\);
(c) \(y'' = (t^3 + 5)y + \sin(t), \qquad y(0) = 0,\qquad y(1) = 1\);
(d) \(y'' = (5y + \sin(3t)) e^t, \qquad y(0) = 0,\qquad y(1) = 0\).
Exercise 5.2
Consider the following boundary value problem
Calculate the Euler method solutions using a step length of \(h=0.2\) and guess values of \(y'(0) = 1\) and \(y'(0) = 2\).
Solution
\(s = 1\):
\(t\) |
\(y_1\) |
\(y_2\) |
|---|---|---|
0.00 |
0.0000 |
1.0000 |
0.20 |
0.2000 |
1.0000 |
0.40 |
0.4000 |
0.8400 |
0.60 |
0.5680 |
0.5200 |
0.80 |
0.6720 |
0.0656 |
1.00 |
0.6851 |
-0.4720 |
\(s = 2\):
\(t\) |
\(y_1\) |
\(y_2\) |
|---|---|---|
0.00 |
0.0000 |
2.0000 |
0.20 |
0.4000 |
2.0000 |
0.40 |
0.8000 |
1.6800 |
0.60 |
1.1360 |
1.0400 |
0.80 |
1.3440 |
0.1312 |
1.00 |
1.3702 |
-0.9440 |
Exercise 5.3
Use the Secant method to calculate a guess value for \(y'(0)\) based on your solutions to the boundary value problem in Exercise 5.2. Calculate the solutions using the Euler method using this new guess value.
Solution
\(s = 1.4596\):
\(t\) |
\(y_1\) |
\(y_2\) |
|---|---|---|
0.00 |
0.0000 |
1.4596 |
0.20 |
0.2919 |
1.4596 |
0.40 |
0.5838 |
1.2261 |
0.60 |
0.8291 |
0.7590 |
0.80 |
0.9809 |
0.0957 |
1.00 |
1.0000 |
-0.6889 |
Exercise 5.4
Calculate the solution of the boundary value problem in Exercise 5.2 using the finite-difference method with a step length \(h=0.2\).
Solution
\(t\) |
\(y\) |
|---|---|
0.00 |
0.0000 |
0.20 |
0.4337 |
0.40 |
0.7981 |
0.60 |
1.0347 |
0.80 |
1.1058 |
1.00 |
1.0000 |
Exercise 5.5
The exact solution to the boundary value problem in Exercise 5.2 is \(y = \dfrac{\sin(2t)}{\sin(2)}\). Produce a plot comparing the solutions to this BVP using the Euler method from Exercise 5.3 and the finite-difference method from Exercise 5.4 against the exact solution.
Solution
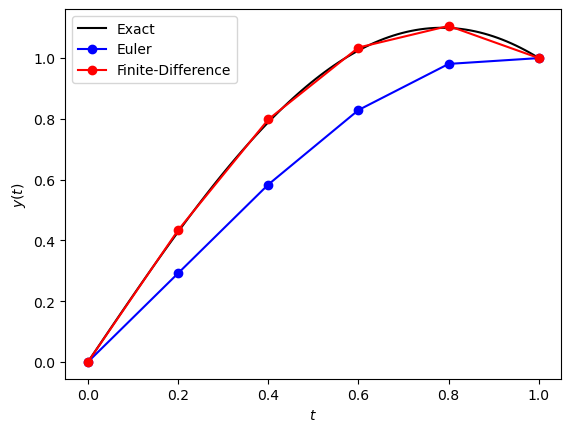
5.4.1. Solutions#
The solutions to these exercises downloaded below by right clicking on the link and select ‘Save Link As’:
