7.4. The Successive Over Relaxation (SOR) method#

The Successive Over Relaxation (SOR) method improves on the convergence rate of the Gauss-Seidel method by applying a weighting factor to the updated estimates to adjust the extent of the change. Let \(\omega\) be a relaxation parameter in the range \([0,2]\) then the SOR method is

Definition 7.5 (The Successive Over Relaxation (SOR) method)

The SOR method for solving a system of linear equations of the form \(A \vec{x} = \vec{b}\) is

(7.9)#\[ x_i^{(k+1)} =(1 - \omega) x_i^{(k)} + \frac{\omega}{a_{ii} }\left(b_i - \sum_{j=1}^{i-1} a_{ij} x_j^{(k+1)} -\sum_{j=i+1}^n a_{ij} x_j^{(k)} \right), \qquad i = 1, \ldots, n. \]

where \(\omega \in [0, 2]\).

7.4.1. The iteration matrix for the SOR method#

The iteration matrix for the SOR method is derived by writing the coefficient matrix of the linear system \(A\vec{x}=\vec{b}\) using

\[ A = L+\left(1-\frac{1}{\omega }\right)D+\frac{1}{\omega }D+U. \]

Substituting into the linear system \(A \vec{x} = \vec{b}\) and rearranging

\[\begin{split} \begin{align*} \left(L+\left(1-\frac{1}{\omega }\right)D+\frac{1}{\omega }D+U\right)\vec{x}&=\vec{b}\\ (D+\omega L)\vec{x}+((\omega -1)D+\omega U)\vec{x}&=\omega \vec{b}\\ (D+\omega L)\vec{x}&=((1-\omega )D-\omega U)\vec{x}+\omega \vec{b}\\ \vec{x}&=(D+\omega L)^{-1} ((1-\omega )D-\omega U)\vec{x}+(D+\omega L)^{-1} \omega \vec{b}. \end{align*} \end{split}\]

So the matrix form of the SOR method is

\[ \vec{x}^{(k+1)} =(D+\omega L)^{-1} ((1-\omega )D-\omega U)\vec{x}^{(k)} +(D+\omega L)^{-1} \omega \vec{b} \]

and the iteration matrix is

(7.10)#\[ T_{SOR} =(D+\omega L)^{-1} ((1-\omega )D-\omega U). \]

7.4.2. Under and over relaxation#

The value of \(\omega\) affects the rate of convergence of the SOR method and is determined by how the Gauss-Seidel method converges to the exact solution. Consider the diagrams in Fig. 7.4 and Fig. 7.5 below that shows the two types of convergence of the Gauss-Seidel method. When we have monotonic convergence where each successive iteration approaches the exact solution from a single side (Fig. 7.4), the rate of convergence is improved by using \(\omega > 1\) so that the change in subsequent approximations is increased. When we have oscillatory convergence where successive iterations overshoot the exact solution (Fig. 7.5) the rate of convergence is improved by using \(\omega < 1\) so that the change in the subsequent approximation is decreased.

../_images/sor_1.svg

Fig. 7.4 The estimated solution approaches the exact solution monotonically.#

../_images/sor_2.svg

Fig. 7.5 The estimated solution oscillates about the exact solution.#

7.4.3. Optimum value of the relaxation parameter#

The optimum value of \(\omega\) will be the one that minimises the spectral radius of the iteration matrix. The iteration matrix will depend on the value of \(\omega\). One way to estimate the optimum value of \(\omega\) is to calculate \(\rho(T_{SOR})\) for values in the range \(\omega \in [0, 2]\) and choose the value of \(\omega\) which minimises this value. This has been done for the system of linear equations from Example 7.1 and the plot is shown in Fig. 7.6.

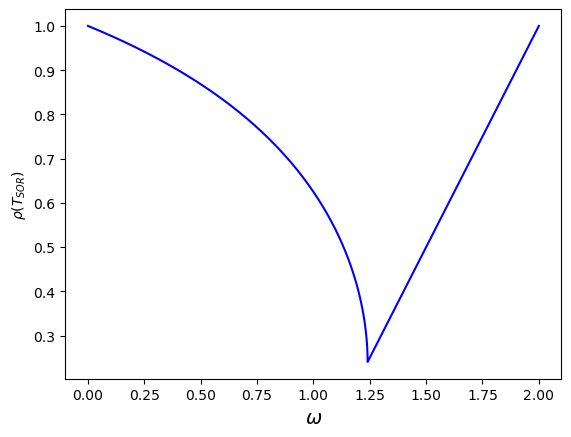
../_images/4e70f214abafe39eb697d65f728471228e3d13a6e3e2c53fff5b0ca4717e5558.png

Fig. 7.6 Plot of the spectral radius \(\rho(T_{SOR})\) of the iteration matrix for the SOR method when used to solve the system of linear equations from Example 7.1.#

So an estimation of the optimum value of the relaxation parameters is \(\omega = 1.25\). If the coefficient matrix \(A\) has real eigenvalues we can use the following theorem to calculate the exact value of \(\omega\).

Theorem 7.2 (Optimum relaxation parameter)

If a system of linear equations of the form \(A\vec{x}=\vec{b}\) has a coefficient matrix \(A\) with all real eigenvalues then the optimum relaxation parameter for the SOR method can be calculated using

(7.11)#\[ \omega_{opt} = 1+{\left(\frac{\rho (T_J )}{1+\sqrt{1-\rho (T_J )^2 }}\right)}^2, \]

where \(\rho(T_J)\) is the spectral radius of the iteration matrix of the Jacobi method calculation using equation (7.4).

Example 7.4

Determine the optimum relaxation parameter for the SOR method when applied to the system of linear equations from Example 7.1 using equation (7.11).

Solution (click to show)

We saw in Example 7.3 that the spectral radius of the iteration matrix for the Jacobi method for this system is \(\rho(T_J )=0.7906\).

Using equation (7.11)

\[ \begin{align*} \omega = 1 + \left( \frac{0.7906}{1 + \sqrt{1 - 0.7906)^2}} \right)^2 \approx 1.2404. \end{align*} \]

Example 7.5

Solve the system of linear equations from from Example 7.1 using the SOR method with \(\omega = 1.24\) and an accuracy tolerance of \(tol = 10^{-4}\)

\[\begin{split} \begin{align*} 4x_1 +3x_2 &=-2,\\ 3x_1 +4x_2 -x_3 &=-8,\\ -x_2 +4x_3 &=14. \end{align*} \end{split}\]
Solution (click to show)

The SOR method for this system is

\[\begin{split} \begin{align*} x_{1}^{(k+1)} &= (1 - \omega)x_{1}^{(k)} + \frac{\omega}{4} \left( -2 - 3 x_{2}^{(k)} \right), \\ x_{2}^{(k+1)} &= (1 - \omega)x_{2}^{(k)} + \frac{\omega}{4} \left( -8 - 3 x_{1}^{(k+1)} + x_{3}^{(k)} \right), \\ x_{3}^{(k+1)} &= (1 - \omega)x_{3}^{(k)} + \frac{\omega}{4} \left( 14 + x_{2}^{(k+1)} \right). \end{align*} \end{split}\]

Using starting values of \(\vec{x} = \vec{0}\). Calculating the first iteration

\[\begin{split} \begin{align*} x_{1}^{(1)} &= (1 - 1.24)(-0.5) \frac{1.24}{4} \left( -2 - 3 (-1.625) \right) = -0.5, \\ x_{2}^{(1)} &= (1 - 1.24)(-1.625) \frac{1.24}{4} \left( -8 - 3 (-0.5) + -3.09375 \right) = -1.625, \\ x_{3}^{(1)} &= (1 - 1.24)(3.09375) \frac{1.24}{4} \left( 14 + 1.625 \right) = 3.09375. \end{align*} \end{split}\]

Calculate the residual

\[\begin{split} \begin{align*} \vec{r}^{(1)} &= \vec{b} - A \vec{x}^{(1)} = \begin{pmatrix} -2 \\ -8 \\ 14 \end{pmatrix} - \begin{pmatrix} 4 & 3 & 0 \\ 3 & 4 & -1 \\ 0 & -1 & 4 \end{pmatrix} \begin{pmatrix} -0.5 \\ -1.625 \\ 3.09375 \end{pmatrix} \\ &= \begin{pmatrix} 4.875 \\ 3.09375 \\ 0.0 \end{pmatrix}. \end{align*} \end{split}\]

Since \(\max(\| \vec{r}^{(1)} \|) = 4.875 > 10^{-4}\) we continue iterating. Calculating the second iteration

\[\begin{split} \begin{align*} x_{1}^{(2)} &= (1 - 1.24)(0.71875) \frac{1.24}{4} \left( -2 - 3 (-1.765625) \right) = 0.71875, \\ x_{2}^{(2)} &= (1 - 1.24)(-1.765625) \frac{1.24}{4} \left( -8 - 3 (0.71875) + -3.05859375 \right) \\ &= -1.765625, \\ x_{3}^{(2)} &= (1 - 1.24)(3.05859375) \frac{1.24}{4} \left( 14 + 1.765625 \right) = 3.05859375. \end{align*} \end{split}\]

Calculate the residual

\[\begin{split} \begin{align*} \vec{r}^{(2)} &= \vec{b} - A \vec{x}^{(1)} = \begin{pmatrix} -2 \\ -8 \\ 14 \end{pmatrix} - \begin{pmatrix} 4 & 3 & 0 \\ 3 & 4 & -1 \\ 0 & -1 & 4 \end{pmatrix} \begin{pmatrix} 0.71875 \\ -1.765625 \\ 3.05859375 \end{pmatrix} \\ &= \begin{pmatrix} 0.421875 \\ -0.03515625 \\ 0.0 \end{pmatrix}. \end{align*} \end{split}\]

Since \(\max(\| \vec{r}^{(2)} \|) = 0.421875 > 10^{-4}\) we continue iterating. The SOR method was iterated until \(\|\vec{r}\| < 10^{-4}\) and the iteration values are given in the table below. Note that the SOR method took 9 iterations to achieve convergence to \(tol=10^{-4}\) whereas the Jacobi method took 49 iterations and the Gauss-Seidel method took 19 iterations to achieve the same accuracy.

\(k\)

\(x_{1}\)

\(x_{2}\)

\(x_{3}\)

\(\max(\| \vec{r} \|)\)

0

0.000000

0.000000

0.000000

14.000000

1

-0.620000

-1.903400

3.749946

6.19e+00

2

1.298962

-2.068735

2.798705

9.90e-01

3

0.992173

-2.038626

3.036337

2.14e-01

4

1.037801

-2.014620

2.986747

1.07e-01

5

1.004524

-2.004807

3.001690

1.16e-02

6

1.003385

-2.001470

2.999139

9.13e-03

7

1.000555

-2.000430

3.000073

9.29e-04

8

1.000267

-2.000122

2.999944

7.01e-04

9

1.000050

-2.000034

3.000003

9.65e-05

7.4.4. Code#

The code below defines a function called sor() which solves a linear system of equations of the for \(A \vec{x} = \vec{b}\) using the SOR method with a relaxation parameter \(\omega\).

def sor(A, b, omega, tol):
    n = len(b)
    x = np.zeros(n)
    for k in range(100):
        for i in range(n):
            sum_ = 0
            for j in range(n):
                if i != j:
                    sum_ += A[i,j] * x[j]
        
            x[i] = (1 - omega) * x[i] + omega * (b[i] - sum_) / A[i,i]
            
        r = b - np.dot(A, x)
        if max(abs(r)) < tol:
            break
    
    return x

function x = sor(A, b, omega, tol)

n = length(b);
x = zeros(n, 1);
for k = 1 : 100
    for i = 1 : n
        sum_ = 0;
        for j = 1 : n
            if j ~= i
                sum_ = sum_ + A(i,j) * x(j);
            end
        end
        x(i) = (1 - omega) * x(i) + omega * (b(i) - sum_) / A(i,i);
    end
    r = b - A * x;
    if max(abs(r)) < tol
        break
    end
end

end