6.5. QR decomposition

QR decomposition is another decomposition method that factorises a matrix in the product of two matrices \(Q\) and \(R\) such that

\[ \begin{align*} A = QR, \end{align*} \]

where \(Q\) is an orthogonal matrix and \(R\) is an upper triangular matrix.

Definition 6.2 (Orthogonal vectors)

A set of vectors \(\lbrace \mathbf{v}_1 ,\mathbf{v}_2 ,\mathbf{v}_3 ,\dots \rbrace\) is said to be orthogonal if \(\mathbf{v}_i \cdot \mathbf{v}_j =0\) for \(i\not= j\). Furthermore the set is said to be orthonormal if \(\mathbf{v}_i\) are all unit vectors.

Definition 6.3 (Orthogonal matrix)

An orthogonal matrix is a matrix where the columns are a set of orthonormal vectors. If \(A\) is an orthogonal matrix if

\[ \begin{align*} A^\mathsf{T} A=I. \end{align*} \]

For example consider the matrix

\[\begin{split} \begin{align*} A= \begin{pmatrix} 0.8 & -0.6\\ 0.6 & 0.8 \end{pmatrix}. \end{align*} \end{split}\]

This is an orthogonal matrix since

\[\begin{split} \begin{align*} A^\mathsf{T} A=\begin{pmatrix} 0.8 & 0.6\\ -0.6 & 0.8 \end{pmatrix} \begin{pmatrix} 0.8 & -0.6\\ 0.6 & 0.8 \end{pmatrix} = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}=I. \end{align*} \end{split}\]

Futhermore it is an orthonormal matrix since the magnitude of the columns for \(A\) are both 1.

---

6.5.1. QR decomposition using the Gram-Schmidt process

Consider the \(3 \times 3\) matrix \(A\) represented as the concatenation of the column vectors \(\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\)

\[\begin{split} \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} = \begin{pmatrix} \uparrow & \uparrow & \uparrow \\ \mathbf{a}_1 & \mathbf{a}_2 & \mathbf{a}_3 \\ \downarrow & \downarrow & \downarrow \end{pmatrix} \end{split}\]

where \(\mathbf{a}_j = (a_{1j}, a_{2j}, a_{3j})\). To calculate the orthogonal \(Q\) matrix we need a set of vectors \(\{\mathbf{q}_1, \mathbf{q}_2, \mathbf{q}_3\}\) that span the same space as \(\{\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3\}\) but are orthogonal to each other. One way to do this is using the Gram-Schmidt process. Consider the diagram shown in Fig. 6.1 that shows the first two non-orthogonal vectors \(\mathbf{a}_1\) and \(\mathbf{a}_2\).

Fig. 6.1 The Gram-Schmidt process

We begin by letting \(\mathbf{u}_1 = \mathbf{a}_1\) and seek to find a vector \(\mathbf{u}_2\) that is orthogonal to \(\mathbf{u}_1\) and in the same span as \(\mathbf{a}_2\). To do this we subtract the vector projection of \(\mathbf{a}_2\) onto \(\mathbf{u}_1\), i.e.,

\[ \mathbf{u}_2 = \mathbf{a}_2 - \left( \frac{\mathbf{q}_1 \cdot \mathbf{a}_1}{\mathbf{q}_1 \cdot \mathbf{u}_1} \right) \mathbf{u}_1.\]

We can simplify things by normalising \(\mathbf{u}_1\) such that \(\mathbf{q}_1 = \dfrac{\mathbf{u}_1}{\|\mathbf{u}_1\|}\) so we have

(6.3)\[ \mathbf{u}_2 = \mathbf{a}_2 - (\mathbf{q}_1 \cdot \mathbf{a}_2) \mathbf{q}_1, \]

which we also normalise to give \(\mathbf{q}_2 = \dfrac{\mathbf{u}_2}{\|\mathbf{u}_2\|}\). For the next vector \(\mathbf{a}_3\) we want the vector \(\mathbf{u}_3\) to be orthogonal to both \(\mathbf{q}_1\) and \(\mathbf{q}_2\) so we subtract both the vector projections of \(\mathbf{a}_3\) onto \(\mathbf{q}_1\) and \(\mathbf{q}_2\)

(6.4)\[ \mathbf{u}_3 = \mathbf{a}_3 - (\mathbf{q}_1 \cdot \mathbf{a}_3) \mathbf{q}_1 - (\mathbf{q}_2 \cdot \mathbf{a}_3) \mathbf{q}_2, \]

which is normalised to give \(\mathbf{q}_3\). Using \(\mathbf{u}_i = (\mathbf{q}_i \cdot \mathbf{a}_i) \mathbf{q}_i\) and rearranging (6.3) and (6.4) to make \(\mathbf{a}_i\) the subject and

\[\begin{split} \begin{align*} \mathbf{a}_1 &= (\mathbf{q}_1 \cdot \mathbf{a}_1), \\ \mathbf{a}_2 &= (\mathbf{q}_1 \cdot \mathbf{a}_2) \mathbf{q}_1 + (\mathbf{q}_2 \cdot \mathbf{a}_2) \mathbf{q}_2, \\ \mathbf{a}_3 &= (\mathbf{q}_1 \cdot \mathbf{a}_3) \mathbf{q}_1 + (\mathbf{q}_2 \cdot \mathbf{a}_3) \mathbf{q}_2 + (\mathbf{q}_3 \cdot \mathbf{a}_3) \mathbf{q}_3, \\ & \vdots \end{align*} \end{split}\]

The columns of the \(Q\) matrix are formed using the vectors \(\mathbf{q}_i\)

\[\begin{split} Q = \begin{pmatrix} \uparrow & \uparrow & & \uparrow \\ \mathbf{q}_1 & \mathbf{q}_2 & \cdots & \mathbf{q}_n \\ \downarrow & \downarrow & & \downarrow \end{pmatrix}, \end{split}\]

and the elements of the \(R\) matrix are formed from the dot products of the \(\mathbf{q}_i\) and \(\mathbf{a}_j\) vectors such that

\[\begin{split} R = \begin{pmatrix} (\mathbf{q}_1 \cdot \mathbf{a}_1) & (\mathbf{q}_1 \cdot \mathbf{a}_2) & \cdots & (\mathbf{q}_1 \cdot \mathbf{a}_n) \\ 0 & (\mathbf{q}_2 \cdot \mathbf{a}_2) & \cdots & (\mathbf{q}_1 \cdot \mathbf{a}_n) \\ \vdots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & (\mathbf{q}_n \cdot \mathbf{a}_n) \end{pmatrix}. \end{split}\]

Positive diagonal elements of \(R\)

It has become standard convention to impose a condition that the diagonal elements of \(R\) must be positive so that we get a unique factorisation. Consider \(A = QR\) then multiplying a column of \(Q\) by \(-1\) and the corresponding row of \(R\) by \(-1\) doesn’t change the product \(QR\). So if any of the diagonal elements of \(R\) are negative we multiply the corresponding column of \(Q\) and row of \(R\) by \(-1\).

Algorithm 6.7 (QR decomposition using the Gram-Schmidt process)

Inputs: An \(m \times n\) matrix \(A\).

Outputs: An \(m \times n\) orthogonal matrix \(Q\) and and \(n \times n\) upper triangular matrix \(R\) such that \(A = QR\).

• For \(j = 1, \ldots, n\) do

  • For \(i = 1, \ldots, j - 1\) do

    • \(r_{ij} \gets \mathbf{q}_i \cdot \mathbf{a}_j\)

  • \(\mathbf{u}_j \gets \mathbf{a}_j - \displaystyle\sum_{i=1}^{j-1} r_{ij} \mathbf{q}_i\)

  • \(r_{jj} \gets \| \mathbf{u}_j \|\)

  • \(\mathbf{q}_j \gets \dfrac{\mathbf{u}_j}{r_{jj}}\)

• \(Q \gets (\mathbf{q}_1, \mathbf{q}_2, \ldots, \mathbf{q}_2)\)

• For \(i = 1, \ldots, n\) do

  • If \(r_{ii} < 0\) then

    • \(R(i,: ) \gets -R(i,:)\)

    • \(Q(:,i) \gets -Q(:,i)\)

• Return \(Q\) and \(R\)

Example 6.8

Calculate the QR decomposition of the following matrix using the Gram-Schmidt process

\[\begin{split} \begin{align*} A = \begin{pmatrix} -1 & -1 & 1 \\ 1 & 3 & 3 \\ -1 & -1 & 5 \\ 1 & 3 & 7 \end{pmatrix}. \end{align*} \end{split}\]

---

Solution

\[\begin{split} \begin{align*} j &= 1: & \mathbf{u}_1 &= \mathbf{a}_1 = \begin{pmatrix} -1 \\ 1 \\ -1 \\ 1 \end{pmatrix}, \\ && r_{11} &= \| \mathbf{u}_1 \| = 2, \\ && \mathbf{q}_1 &= \frac{\mathbf{u}_1}{r_{11}} = \frac{1}{2} \begin{pmatrix} -1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \end{pmatrix}. \\ j &= 2: & r_{12} &= \mathbf{q}_1 \cdot \mathbf{a}_2 = \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \end{pmatrix} \cdot \begin{pmatrix} -1 \\ 3 \\ -1 \\ 3 \end{pmatrix} = 4, \\ && \mathbf{u}_2 &= \mathbf{a}_2 - r_{12} \mathbf{q}_1 = \begin{pmatrix} -1 \\ 3 \\ -1 \\ 3 \end{pmatrix} - 4 \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix}, \\ && r_{22} &= \| \mathbf{u}_2 \| = 2, \\ && \mathbf{q}_2 &= \frac{\mathbf{u}_2}{r_{22}} = \frac{1}{2} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{pmatrix}. \\ j &= 3: & r_{13} &= \mathbf{q}_1 \cdot \mathbf{a}_3 = \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 3\\ 5 \\ 7 \end{pmatrix} = 2, \\ && r_{23} &= \mathbf{q}_2 \cdot \mathbf{a}_3 = \begin{pmatrix} \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 3 \\ 5 \\ 7 \end{pmatrix} = 8, \\ && \mathbf{u}_3 &= \mathbf{a}_3 - r_{13} \mathbf{q}_1 - r_{23} \mathbf{q}_2 = \begin{pmatrix} 1 \\ 3 \\ 5 \\ 7 \end{pmatrix} - 2 \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \end{pmatrix} - 8 \begin{pmatrix} \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{pmatrix} = \begin{pmatrix} -2 \\ -2 \\ 2 \\ 2 \end{pmatrix}, \\ && r_{33} &= \| \mathbf{u}_3 \| = 4, \\ && \mathbf{q}_3 &= \frac{\mathbf{u}_3}{r_{33}} = \frac{1}{4} \begin{pmatrix} -2 \\ -2 \\ 2 \\ 2 \end{pmatrix} = \begin{pmatrix} -\frac{1}{2} \\ -\frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{pmatrix}. \end{align*} \end{split}\]

The diagonal elements of \(R\) are all positive so we don’t need to make any adjustments. Thus the \(Q\) and \(R\) matrices are given by

\[\begin{split} \begin{align*} Q &= \begin{pmatrix} -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{pmatrix}, & R &= \begin{pmatrix} 2 & 4 & 2 \\ 0 & 2 & 8 \\ 0 & 0 & 4 \end{pmatrix}. \end{align*} \end{split}\]

We can check that this is correct by verifying that \(A = QR\) and that \(Q^\mathsf{T}Q = I\).

\[\begin{split} \begin{align*} \begin{pmatrix} -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} 2 & 4 & 2 \\ 0 & 2 & 8 \\ 0 & 0 & 4 \end{pmatrix} &= \begin{pmatrix} -1 & -1 & 1 \\ 1 & 3 & 3 \\ -1 & -1 & 5 \\ 1 & 3 & 7 \end{pmatrix} = A, \\ \begin{pmatrix} -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{pmatrix} &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = I. \end{align*} \end{split}\]

Code

The code below defines a function called qr_gramschmidt() which calculates the QR decomposition of a matrix A using the Gram-Schmidt process.

Python

def qr_gramschmidt(A):

    n = A.shape[1]
    Q, R = np.copy(A).astype(float), np.zeros((n,n))

    for j in range(n):
        for i in range(j):
            R[i,j] = np.dot(Q[:,i], A[:,j])
            Q[:,j] = Q[:,j] - R[i,j] * Q[:,i]
        
        R[j,j] = np.linalg.norm(Q[:,j])
        Q[:,j] = Q[:,j] / R[j,j]

    for i in range(n):
        if R[i,i] < 0:
            R[i,:] *= -1
            Q[:,i] *= -1

    return Q, R

MATLAB

function [Q, R] = qr_gramschmidt(A)

[~, n] = size(A);
Q = A;
R = zeros(n, n);

for j = 1 : n
    for i = 1 : j - 1
        R(i,j) = dot(Q(:,i), A(:,j));
        Q(:,j) = Q(:,j) - R(i,j) * Q(:,i);
    end

    R(j,j) = norm(Q(:,j));
    Q(:,j) = Q(:,j) / R(j,j);
end

for i = 1 : n
    if R(i,i) < 0
        R(i,:) = -R(i,:);
        Q(:,i) = -Q(:,i);
    end
end

end

6.5.2. QR decomposition using Householder reflections

Another method we can use to calculate the QR decomposition of a matrix is by the use of Householder reflections.

Definition 6.4 (Householder matrix)

The Householder matrix is an orthogonal reflection matrix of the form

(6.5)\[ H = I - 2 \frac{\mathbf{v} \mathbf{v}^\mathsf{T}}{\mathbf{v}^\mathsf{T} \mathbf{v}}, \]

where \(\mathbf{v}\) is a non-zero column vector. The matrix \(H\) is symmetric and orthogonal.

Fig. 6.2 The vector \(\mathbf{x}\) is reflected about the dashed line so that it is parallel to the basis vector \(\mathbf{e}_1\).

Consider the diagram in Fig. 6.2 where the vector \(\mathbf{x}\) is reflected about the hyperplane represented by the dashed line so that it is parallel to the first basis vector of the standard basis \(\mathbf{e}_1 = (1, 0, \ldots, 0)^\mathsf{T}\). The Householder matrix that achieves this reflection is written in terms of the vector \(\mathbf{v}\) which is orthogonal to the dashed line and calculated using

\[ \mathbf{v} = \mathbf{x} - \|\mathbf{x}\|\mathbf{e}_1. \]

If the magnitude of \(\mathbf{x}\) is close to being parallel to \(\mathbf{e}_1\) then \(\mathbf{v}\) will be close to \(\mathbf{0}\) and the calculation of (6.5) will involve the division by a number close to zero. To overcome this we use a Householder transformation to reflect \(\mathbf{x}\) so that it is parallel to \(-\mathbf{e}_1\) instead of \(+\mathbf{e}_1\).

Fig. 6.3 The vector \(\mathbf{x}\) is reflected about the dashed line so that it is parallel to the basis vector \(-\mathbf{e}_1\).

To do this we calculate \(\mathbf{v}\) by adding \(\| \mathbf{x} \| \mathbf{e}_1\) to \( \mathbf{x}\) when the sign of \(x_1\) is negative, i.e.,

\[ \mathbf{v} = \mathbf{x} - \operatorname{sign}(x_1) \| \mathbf{x} \| \mathbf{e}_1, \]

where \(\operatorname{sign}(x)\) returns \(+1\) if \(x \geq 0\) and \(-1\) if \(x < 0\). To compute the QR decomposition of a matrix \(A\), we reflect the first column of \(A\), using Householder reflection so that it is parallel to \(\mathbf{e}_1\). This means that \(r_{11}\) is the only non-zero element in the first column of \(R\).

\[\begin{split} \begin{align*} R = H_1 A = \begin{pmatrix} r_{11} & r_{12} & r_{13} & \cdots & r_{1n} \\ 0 & b_{22} & b_{23} & \cdots & b_{2n} \\ 0 & b_{32} & b_{33} & \cdots & b_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & b_{m2} & b_{m3} & \cdots & b_{mn} \end{pmatrix} \end{align*} \end{split}\]

We then look to do the same for the sub-matrix of \(R\) formed by omitted its first row and column. We do this by calculating a \((m-1) \times (m-1)\) Householder matrix \(H'\) using the second column of \(R\) starting from the diagonal element, i.e., \(\mathbf{x} = (b_{22}, b_{32}, \ldots, b_{m2})^\mathsf{T}\). This is used to form the \(m \times m\) Householder matrix \(H_2\) by padding out the first row and column of the identity matrix.

\[\begin{split} \begin{align*} H_2 = \begin{pmatrix} 1 & \begin{matrix} 0 & \cdots & 0 \end{matrix} \\ \begin{matrix} 0 \\ \vdots \\ 0 \end{matrix} & H' \end{pmatrix} \end{align*} \end{split}\]

The Householder matrix \(H_2\) is then applied to \(R\) so that the elements of the second column below the diagonal are zeroed out.

\[\begin{split} \begin{align*} R = H_2 R = \begin{pmatrix} r_{11} & r_{12} & r_{13} & \cdots & r_{1n} \\ 0 & r_{22} & r_{23} & \cdots & r_{2n} \\ 0 & 0 & c_{33} &\cdots & c_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & c_{n3} & \cdots & c_{nn} \end{pmatrix} \end{align*} \end{split}\]

We repeat this process until column \(j = m - 1\) when \(R\) will be an upper triangular matrix. If \(A\) has \(n\) columns then

\[R = H_{m-1}\ldots H_2 H_1 A,\]

rearranging gives

\[\begin{align*} H_1^{-1} H_2^{-1} \ldots H_{m-1}^{-1} R = A. \end{align*} \]

The Householder matrices are symmetric and orthogonal so \(H^{-1} = H\) and since we want \(A = QR\) then

\[ \begin{align*} Q = H_1H_2 \ldots H_{m-1}. \end{align*} \]

Algorithm 6.8 (QR decomposition using Householder reflections)

Inputs: An \(m \times n\) matrix \(A\).

Outputs: An \(n \times n\) orthogonal matrix \(Q\) and and \(n \times n\) upper triangular matrix \(R\) such that \(A = QR\).

• \(Q \gets I_m\)

• \(R \gets A\)

• For \(j = 1, \ldots, m - 1\) do

  • \(\mathbf{x} \gets\) column \(j\) of \(R\) starting at the \(j\)-th row

  • \(\mathbf{v} \gets \mathbf{x} - \operatorname{sign} (x_1) \|\mathbf{x}\|\mathbf{e}_1\)

  • \(H' \gets I_{m-j+1} - 2 \dfrac{\mathbf{v} \mathbf{v} ^\mathsf{T}}{\mathbf{v}^\mathsf{T} \mathbf{v}}\)

  • \(H(j:m, j:m) \gets H'\) with the first \(j-1\) rows and columns of \(H\) set to those of \(I_m\)

  • \(R \gets H R\)

  • \(Q \gets Q H\)

• For \(i = 1, \ldots, n\) do

  • If \(R(i,i) < 0\) then

    • \(R(i,: ) \gets -R(i,:)\)

    • \(Q(:,i) \gets -Q(:,i)\)

• Return \(Q\) and \(R\).

Example 6.9

Calculate the QR decomposition of the following matrix using Householder reflections

\[\begin{split} \begin{align*} A=\begin{pmatrix} 1 & -4 \\ 2 & 3 \\ 2 & 2 \end{pmatrix}. \end{align*} \end{split}\]

---

Solution

Set \(Q = I\) and \(R = A\). We want to zero out the elements below \(R(1,1)\) so \(\mathbf{x} = (1, 2, 2)^\mathsf{T}\) and \(\|\mathbf{x}\| = 3\).

\[\begin{split} \begin{align*} j &= 1: & \mathbf{x} &= \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}, \\ && \mathbf{v} &= \mathbf{x} - \operatorname{sign}(x_1) \|\mathbf{x}\| \mathbf{e}_1 = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} - 3 \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -2 \\ 2 \\ 2 \end{pmatrix}, \\ && H &= I - 2 \frac{\mathbf{v} \mathbf{v}^\mathsf{T}}{\mathbf{v}^\mathsf{T} \mathbf{v}} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} - \frac{2}{12} \begin{pmatrix} 4 & -4 & -4 \\ -4 & 4 & 4 \\ -4 & 4 & 4 \end{pmatrix} = \begin{pmatrix} \frac{1}{3} & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{1}{3} & -\frac{2}{3} \\ \frac{2}{3} & -\frac{2}{3} & \frac{1}{3} \end{pmatrix}, \\ && R &= H R = \begin{pmatrix} \frac{1}{3} & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{1}{3} & -\frac{2}{3} \\ \frac{2}{3} & -\frac{2}{3} & \frac{1}{3} \end{pmatrix} \begin{pmatrix} 1 & -4 \\ 2 & 3 \\ 2 & 2 \end{pmatrix} = \begin{pmatrix} 3 & 2 \\ 0 & -3 \\ 0 & -4 \end{pmatrix}, \\ && Q &= QH = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \frac{1}{3} & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{1}{3} & -\frac{2}{3} \\ \frac{2}{3} & -\frac{2}{3} & \frac{1}{3} \end{pmatrix} = \begin{pmatrix} \frac{1}{3} & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{1}{3} & -\frac{2}{3} \\ \frac{2}{3} & -\frac{2}{3} & \frac{1}{3} \end{pmatrix}. \\ j &= 2: & \mathbf{x} &= \begin{pmatrix} -3 \\ -4 \end{pmatrix}, \\ && \mathbf{v} &= \mathbf{x} - \operatorname{sign}(x_1) \|\mathbf{x}\| \mathbf{e}_1 = \begin{pmatrix} -3 \\ -4 \end{pmatrix} + 5 \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ -4 \end{pmatrix}, \\ && H' &= I - 2 \frac{\mathbf{v}\mathbf{v}^\mathsf{T}}{\mathbf{v}^\mathsf{T} \mathbf{v}} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - \frac{2}{20} \begin{pmatrix} 4 & -8 \\ -8 & 16 \end{pmatrix} = \begin{pmatrix} \frac{3}{5} & \frac{4}{5} \\ \frac{4}{5} & -\frac{3}{5} \end{pmatrix}, \\ && H &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{3}{5} & \frac{4}{5} \\ 0 & \frac{4}{5} & -\frac{3}{5} \end{pmatrix}, \\ && R &= H R = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -\frac{3}{5} & -\frac{4}{5} \\ 0 & -\frac{4}{5} & \frac{3}{5} \end{pmatrix} \begin{pmatrix} 3 & 2 \\ 0 & 3 \\ 0 & -4 \end{pmatrix} = \begin{pmatrix} 3 & 2 \\ 0 & -5 \\ 0 & 0 \end{pmatrix}, \\ && Q &= Q H = \begin{pmatrix} \frac{1}{3} & \frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{2}{3} & -\frac{1}{3} \\ \frac{2}{3} & -\frac{1}{3} & \frac{2}{3} \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \frac{3}{5} & \frac{4}{5} \\ 0 & \frac{4}{5} & -\frac{3}{5} \end{pmatrix} = \begin{pmatrix} \frac{1}{3} & \frac{14}{15} & \frac{2}{15} \\ \frac{2}{3} & -\frac{1}{3} & \frac{2}{3} \\ \frac{2}{3} & -\frac{2}{15} & -\frac{11}{15} \end{pmatrix}. \end{align*} \end{split}\]

The second diagonal element of \(R\) is negative, so we multiply row 2 of \(R\) and column 2 of \(Q\) by \(-1\)

\[\begin{split} \begin{align*} Q &= \begin{pmatrix} \frac{1}{3} & -\frac{14}{15} & \frac{2}{15} \\ \frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{2}{15} & -\frac{11}{15} \end{pmatrix}, & R &= \begin{pmatrix} 3 & 2 \\ 0 & 5 \\ 0 & 0 \end{pmatrix}. \end{align*} \end{split}\]

We can check whether this is correct by verifying that \(A = QR\) and \(Q^\mathsf{T} Q = I\).

\[\begin{split} \begin{align*} QR &= \begin{pmatrix} \frac{1}{3} & -\frac{14}{15} & \frac{2}{15} \\ \frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{2}{15} & -\frac{11}{15} \end{pmatrix} \begin{pmatrix} 3 & 2 \\ 0 & 5 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 1 & -4 \\ 2 & 3 \\ 2 & 2 \end{pmatrix} = A, \\ Q^\mathsf{T} Q &= \begin{pmatrix} \frac{1}{3} & \frac{2}{3} & \frac{2}{3} \\ -\frac{14}{15} & \frac{1}{3} & \frac{2}{15} \\ \frac{2}{15} & \frac{2}{3} & -\frac{11}{15} \end{pmatrix} \begin{pmatrix} \frac{1}{3} & -\frac{14}{15} & \frac{2}{15} \\ \frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{2}{15} & -\frac{11}{15} \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = I. \end{align*} \end{split}\]

Code

The code below defines a function called qr_householder() that calculates the QR decomposition of an \(m \times n\) matrix \(A\) using Householder reflections. This has been used to calculate the QR decomposition of the matrix from Example 6.9.

Python

def qr_householder(A):
    
    m, n = A.shape
    Q, R = np.eye(m), np.copy(A).astype(float)

    for i in range(m - 1):
        x = R[i:,i]
        v = np.array([x + np.sign(x[0]) *  np.linalg.norm(x) * np.eye(m - i)[:,0]]).T
        H = np.eye(m)
        H[i:,i:] -= 2 * np.dot(v, v.T) / np.dot(v.T, v)
        R = np.dot(H, R)
        Q = np.dot(Q, H)

    for i in range(n):
        if R[i,i] < 0:
            R[i,:] *= -1
            Q[:,i] *= -1

    return Q, R

MATLAB

function [Q, R] = qr_householder(A)

[m, n] = size(A);
Q = eye(m);
R = A;

for i = 1 : m - 1
    x = R(i:end,i);
    if sign(x(1)) > 0
        v = x + norm(x) * [1 ; zeros(m-i,1)];
    else
        v = x - norm(x) * [1 ; zeros(m-i,1)];
    end
    H = eye(m);
    H(i:end,i:end) = H(i:end,i:end) - 2 * v * v' / dot(v, v);
    R = H * R;
    Q = Q * H;
end

for i = 1 : n
    if R(i,i) < 0
        R(i,:) = -R(i,:);
        Q(:,i) = -Q(:,i);
    end
end

end

---

6.5.3. Loss of orthogonality

Like any numerical technique, the QR decomposition methods shown here are prone to computational rounding errors. If \(Q\) is perfectly orthogonal then \(Q^\mathsf{T}Q = I\), but if there is bound to be some small error. If we let this error be \(E\) then \(Q^\mathsf{T}Q = I + E\). Rearranging gives

\[ \| Q^\mathsf{T}Q - I\| = E,\]

which is known as the Frobenius norm and is a measure of the loss of orthogonality.

The both QR decomposition methods shown here use an iterative approach where we orthogonalised the columns of the \(A\) matrix in turn based upon the previous iterations. So an error in column \(i\) will have a knock on effect on all subsequent columns. To analyse the methods, the QR decomposition of a random \(200 \times 200\) matrix \(A\) was computed using the Gram-Schmidt process and Householder reflections. The Frobenius norm was calculated for the first \(n\) columns of \(Q\) where \(n = 1 \ldots 200\) giving the loss of orthogonality for those iterations and plotted in below.

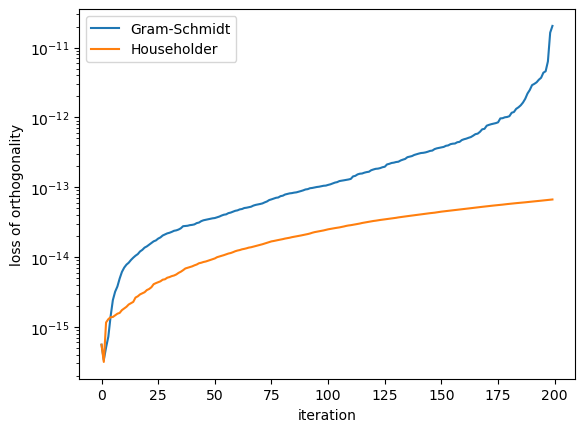
Here we can see that computing QR decomposition using Householder reflections is less prone to orthogonality errors than using the Gram-Schmidt process.