4.6. Stability exercises

Exercise 4.1

Determine the stability function of the following Runge-Kutta method

\[\begin{split} \begin{array}{c|ccccc} 0 & 0 & & & & \\ \frac{1}{4} & \frac{1}{4} & & & & \\ \frac{1}{2} & \frac{1}{2} & 0 & & & \\ 3/4 & 0 & \frac{1}{2} & \frac{1}{4} & & \\ 0 & 0 & \frac{1}{6} & -\frac{1}{3} & \frac{1}{6} & \\ \hline & -1 & \frac{2}{3} & -\frac{1}{3} & \frac{2}{3} & 1 \end{array} \end{split}\]

Solution

\[ R(z) = 1 + z + \frac{1}{2}z + \frac{1}{6}z^3 + \frac{1}{24}z^4 \]

Exercise 4.2

Determine the stability function of the following Runge-Kutta method. Is this an A-stable method?

\[\begin{split} \begin{array}{c|cc} \frac{1}{4} & \frac{7}{24} & -\frac{1}{24} \\ \frac{3}{4} & \frac{13}{24} & \frac{5}{24} \\ \hline & \frac{1}{2} & \frac{1}{2} \end{array} \end{split}\]

Solution

\[R(z) = \frac{1 + \frac{1}{2}z + \frac{1}{12}z^2}{1 - \frac{1}{2}z + \frac{1}{12}z^2}\]

The roots of \(Q(z)\) are \(3 \pm \sqrt{3}i\) and \(E(y) = 0\) so this is an A-stable method.

Exercise 4.3

Plot the region of absolute stability for the fourth-order Gauss-Legendre method. What does your plot suggest about the method?

\[\begin{split} \begin{array}{c|cc} \frac{1}{2} - \frac{\sqrt{3}}{6} & \frac{1}{4} & \frac{1}{4} - \frac{\sqrt{3}}{6} \\ \frac{1}{2} + \frac{\sqrt{3}}{6} & \frac{1}{4} + \frac{\sqrt{3}}{6} & \frac{1}{4} \\ \hline & \frac{1}{2} & \frac{1}{2} \end{array} \end{split}\]

Solution

\[R(z) = \frac{1 + \frac{1}{2}z + \frac{1}{12}z^2}{1 - \frac{1}{2}z + \frac{1}{12}z^2}\]

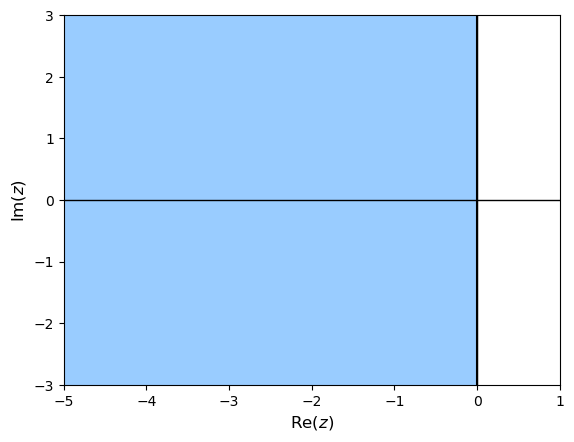
This is an A-stable method.

Exercise 4.4

Calculate the stiffness ratio for the following system of ODEs.

\[\begin{align*} y_1' &= -20y_1 + y_2, \\ y_2' &= 500 y_2. \end{align*}\]

For the Euler method with step size \(h = 0.05\), test the stability against both of the Eigenvalues of this system.

Solution

The eigenvalues are \(\lambda_1 = -20\) and \(\lambda_2 = -500\) so the stiffness ratio is

\[ S = \frac{-500}{-20} = 25. \]

The stability function for the Euler method is \(R(z) = 1 + z = 1 + h \lambda\). For stability, \(|1 + h \lambda| \leq 1\).

For \(\lambda_1\), \(|R(-25 h)| = |1 - 25(0.05)| = 0 < 1\) so is stable.

For \(\lambda_2\), \(|R(-500 h)| = |1 - 500(0.05)| = 24 > 1\) so is unstable.