1.5. ODEs Exercises#

Exercise 1.1

An IVP is given by

\[\begin{align*} y' + y = 1 - e^{-t} \qquad t\in [0,4], \qquad y(0) = 1. \end{align*}\]

(a)   Using Python or MATLAB, compute the solution to the IVP using the Euler method with a step length of \(h = 0.4\). Produce a plot of the solution \(y(t)\) against \(t\) and the exact solution which is \(y = 1 - te^{-t}\) on the same set of axes.

Solution
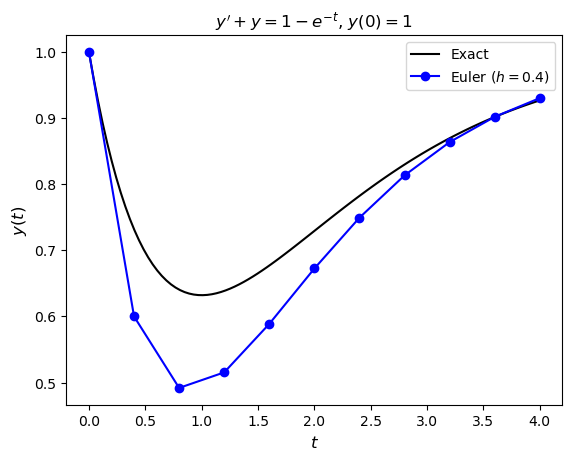
../_images/c97414bf542ce4354fc88f2ede7cf1954ae21a599b724f115a0bcdf694889e15.png

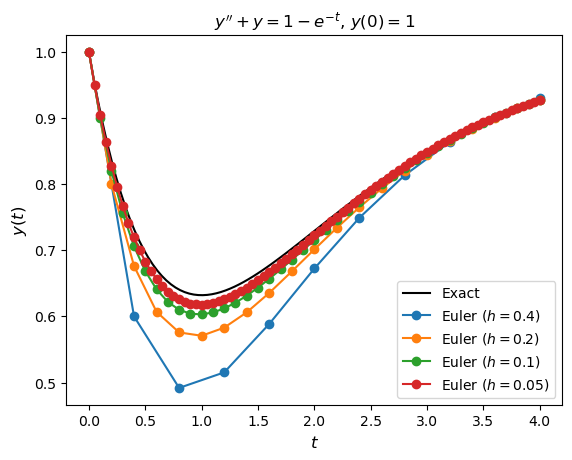
(b)   Compute the solution to this IVP using step lengths of \(h = 0.4, 0.2, 0.1, 0.05\). Produce a plot of the four numerical solutions and the exact solution on the same axes.

Solution
../_images/966ff82da256f92c1f358715e346b62df132a6afe520ed7fd4e9874b814a104e.png

(c)   Calculate the global truncation errors for the four solutions at \(t = 2\). Present your results in the form of a table with columns for the value of \(h\), the numerical solution for \(y(2)\) and the global truncation error \(E\).

Hint: you can use the NumPy command idx = np.argmin(abs(t - 2)) or the MATLAB command [~,idx] = min(abs(t - 2)) to determine the index of the value in the array t which is closest to 2.

Solution
|  h   |  Euler   |   GTE    |
|------|----------|----------|
| 0.40 | 0.672496 | 5.68e-02 |
| 0.20 | 0.701442 | 2.79e-02 |
| 0.10 | 0.715579 | 1.38e-02 |
| 0.05 | 0.722507 | 6.82e-03 |

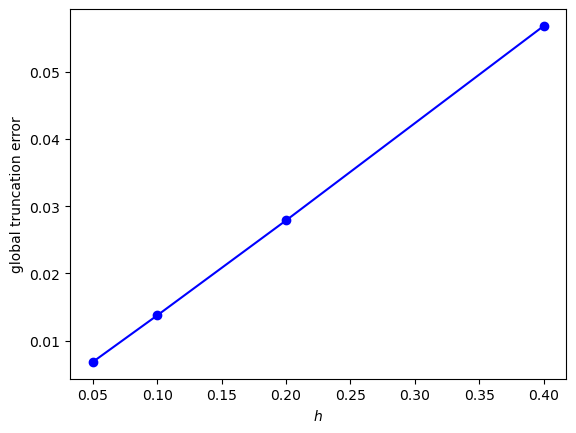
(d)   Produce plot of the global truncation errors \(E\) against the step length \(h\).

Solution
../_images/4c6ee2cf0970135b1d4323254b529d38d960979668959cba249165e8eb973568.png

Exercise 1.2

The motion of a pendulum can be modelled by the following ODE

\[ \begin{align*} \ddot{\theta} + \frac{g}{L} \sin(\theta) = 0, \end{align*} \]

where \(\theta\) is the angle between the pendulum and the vertical, \(L\) is the length of the pendulum and \(g=9.81\text{ms}^{-2}\) is the acceleration due to gravity.

../_images/pendulum.svg

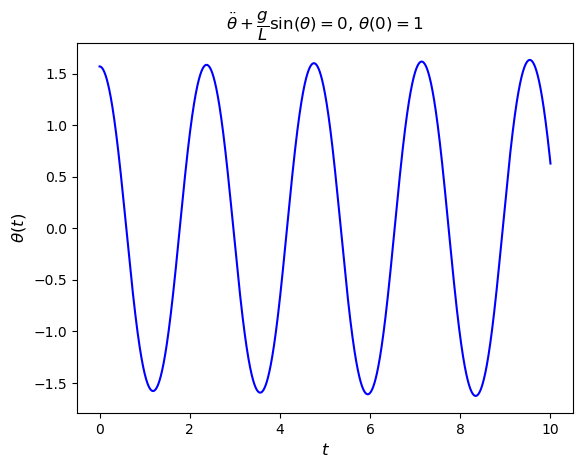
A pendulum of length 1 m is intially set so that the angle between the chord and the vertical is \(\dfrac{\pi}{2}\). Use the Euler method with a step length of \(h = 0.001\) to model the first 10 seconds of the motion of the pendulum. Produce a plot of the displacement angle \(\theta\) against \(t\).

Solution
../_images/e285d2149fa6882576a25fca77d7599e382ae0adefef388b0a8c4fdbe761abe7.png

Exercise 1.3

The Lotka-Volterra equations is a model of predator-prey interactions

\[\begin{split} \begin{align*} \frac{\mathrm{d}x}{\mathrm{d}t} &= ax - bxy, \\ \frac{\mathrm{d}y}{\mathrm{d}t} &= -cy + dxy, \end{align*} \end{split}\]

where \(x\) and \(y\) are the population densities of the prey and predator species respectively, \(a\) and \(b\) are the parameters that govern the birth and death rate of the prey species, and \(c\) and \(d\) are parameters that govern the birth and death rates of the predator species.

(a)   In a given square kilometer the population of rabbits (\(x\)) and foxes (\(y\)) is known to be \(x(0) = y(0) = 5\). Given the the birth and death rates is 0.1 and 0.02 for the rabbit population and 0.04 and 0.04 for the fox population, use the Lotka-Volterra to model the population of the two species over a time frame of \([0, 100]\). Produce a plot of the population of both species on the same set of axes.

Solution
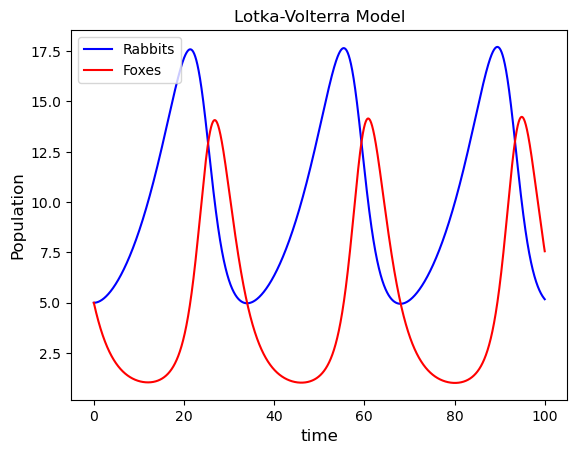
../_images/e51526f34b030edef42428771aadad11e61d389eec08f7615645c766592eb857.png

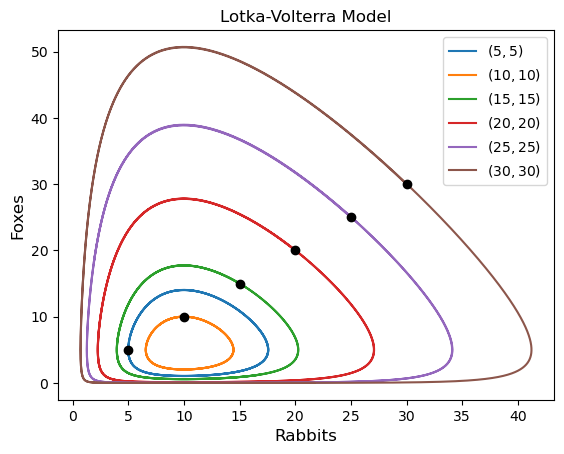
(b)   Repeat the calculations with the initial populations \(x(0) = y(0) = 5\) and increasing by 5 each time until \(x(0) = y(0) = 30\). Produce a plot of the fox population against the rabbit population for each solution on the same set of axes (known as a phase-space plot).

Solution
../_images/b5e06f7bee5d9fed34d47dae3888894475d7cd0d80b642c1fa9e99c004004705.png