1.3. Systems of ODEs#

So far we have only looked at the solution of a single ODE. In most practical cases, a system of multiple ODEs is required to model a real-world situation. Recall that a single first-order ODE is expressed as a function of the single independent variable \(t\) and a dependent function \(y\)

\[ y' = f(t, y). \]

A system of first-order ODEs is expressed as a set of multiple ODEs such that

\[\begin{split} \begin{align*} y_1' &= f_1(t, y_1, y_2, \ldots, y_N), \\ y_2' &= f_2(t, y_1, y_2, \ldots, y_N), \\ & \vdots \\ y_N' &= f_N(t, y_1, y_2, \ldots, y_N), \end{align*} \end{split}\]

where \(y_1, y_2, \ldots, y_N\) are multiple dependent functions. An IVP involving a system of ODEs requires an initial value for each equation in the system, i.e., \(y_1(t_0) = a_1\), \(y_2(t_0) = a_2\) etc. where \(a_1, a_2, \ldots, a_N\) are constants.

To apply a numerical method to solve a system of ODEs, we can write it in vector form \(\mathbf{y}' = \mathbf{f}(t, \mathbf{y})\) where

\[\begin{split} \begin{align*} \vec{y} &= (y_1, y_2, \ldots, y_N), \\ \vec{f}(t, \vec{y}) &= (f_1(t, \vec{y}), f_2(t, \vec{y}), \ldots, f_N(t, \vec{y}). \end{align*} \end{split}\]

Recall that the Euler method for solving an IVP for a single ODE is

\[ y_{n+1} = y_n + h f(t_n, y_n), \]

then for solving a system of first-order ODEs we have

\[ \begin{align*} \vec{y}_{n+1} &= \vec{y}_n + h \vec{f}(t_n, \vec{y}_n). \end{align*} \]

Example 1.2

The SIR model is a simple model that describes the spread of an infectious disease in a population. The model divides the population into three compartments: those who have not yet contracted the disease but are susceptible (\(S\)) those who are infected (\(I\)) and those who have recovered and gained immunity (\(R\)). The formulation of the model is

\[\begin{split} \begin{align*} \dydt{S}{t} &= -\frac{\beta}{N} IS, \\ \dydt{I}{t} & =\frac{\beta}{N} IS - \gamma I, \\ \dydt{R}{t} &= \gamma I, \end{align*} \end{split}\]

where \(N = S + I + R\) is the total population, \(\beta\) is the infection rate in the number of people per day who become infected, and \(\gamma\) is the recovery rate at which a person who is infected recovers per day.

A disease breaks out in a population where \(\beta = 0.5\), \(\gamma = 0.1\) and \(S(0) = 99\), \(I(0) = 1\) and \(R(0) = 0\). Calculate the solution to the SIR model over the first 50 days using the Euler method with a (relatively large) step length of \(h = 1\).

Solution (click to show)

Let \(y_1 = S\), \(y_2 = I\) and \(y_3 = R\) and writing the SIR model in vector form we have

\[\begin{split} \begin{align*} \mathbf{y} &= (y_1, y_2, y_2), \\ \mathbf{f}(t, \mathbf{y}) &= \left( -\frac{\beta}{N} y_1 y_2, \quad \frac{\beta}{N} y_1 y_2 - \gamma y_2 , \quad \gamma y_3 \right). \end{align*} \end{split}\]

The initial conditions are \(\mathbf{y}_0 = (99, 1, 0)\) and \(N = 100\). Calculating the first few steps fo the Euler method with \(h = 1\)

\[\begin{split} \begin{align*} \mathbf{y}_1 &= \mathbf{y}_0 + h \mathbf{f}(t_0, \mathbf{y}_0) \\ &= (99, 1, 0) + 1 ( -0.005 (99)(1), \quad 0.005 (99)(1) - 0.1(0), \quad 0.1(0) ) \\ &= (98.505, 1.395, 0.1), \\ t_1 &= t_0 + h = 0 + 1 = 1, \\ \\ \mathbf{y}_2 &= \mathbf{y}_1 + h \mathbf{f}(t_1, \mathbf{y}_1) \\ &= (98.505, 1.395, 0.1) + 1 (-0.005 (98.505)(1.395), \quad 0.005 (98.505)(1.395) - 0.1(0.1), \quad 0.1(0)) \\ &= (97.8179, 1.9426, 0.2395), \\ t_2 &= t_1 + h = 1 + 1 = 2, \\ \\ \mathbf{y}_3 &= \mathbf{y}_2 + h \mathbf{f}(t_2, \mathbf{y}_2) \\ &= (97.8179, 1.9426, 0.2395) + 1 (-0.005 (97.8179)(1.9426), \quad 0.005 (97.8179)(1.9426) - 0.1(0.2395), \quad 0.1(0)) \\ &= (96.8678, 2.6984, 0.4338), \\ t_3 &= t_2 + h = 2 + 1 = 3, \\ \end{align*} \end{split}\]

The plot of the solutions to the SIR model using the Euler method for the first 50 days of the infection is shown in Fig. 1.9

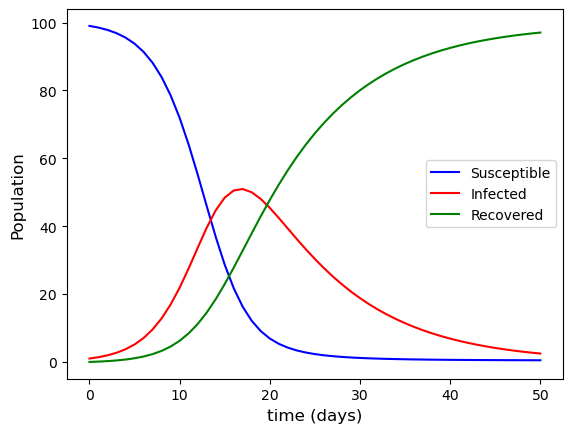
Euler method solutions for the SIR model

Fig. 1.9 Euler method solutions for the SIR model with \(S(0) = 99\), \(I(0) = 1\), \(R(0) = 0\), \(\beta = 0.5\) and \(\gamma = 1\).#

1.3.1. Code#

The function euler() which computes the solutions to a system of ODEs using the Euler method is shown below. This is very similar to the function used to solve a single ODE with the exception that y is initialised to be an \(nsteps \times N\) array if we have \(N\) equations in the system. The first row of y is set equal to the initial values y0 and calculate the Euler method for all values across the rows.

def euler(f, tspan, y0, h):

    nsteps = int((tspan[1] - tspan[0]) / h)
    t = np.zeros(nsteps + 1)
    if (type(y0) is list):
        y = np.zeros((nsteps + 1, len(y0)))
    else:
        y = np.zeros((nsteps + 1, 1))

    t[0] = tspan[0]
    y[0,:] = y0
    
    for n in range(nsteps):
        y[n+1,:] = y[n,:] + h * f(t[n], y[n,:])
        t[n+1] = t[n] + h

    return t, y

function [t, y] = euler(f, tspan, y0, h)

nsteps = floor((tspan(2) - tspan(1)) / h);
t = zeros(nsteps + 1, 1);
if length(y0) > 1
    y = zeros(length(t), length(y0));
else
    y = zeros(length(t), 1);
end
y(1,:) = y0;

for n = 1 : length(t) - 1
    y(n+1,:) = y(n,:) + h * f(t(n), y(n, :));
    t(n+1) = t(n) + h;
end

end

The code below sets up and solves the SIR model example from Example 1.2 using the Euler method

import numpy as np
import matplotlib.pyplot as plt

# Define Euler method function
def euler(f, tspan, y0, h):

    nsteps = int((tspan[1] - tspan[0]) / h)
    t = np.zeros(nsteps + 1)
    y = np.zeros((nsteps + 1, len(y0)))
    t[0] = tspan[0]
    y[0,:] = y0
    
    for n in range(nsteps):
        y[n+1,:] = y[n,:] + h * f(t[n], y[n,:])
        t[n+1] = t[n] + h

    return t, y


# Define SIR model
def SIR(t, y):
    S, I, R = y
    N = S + I + R
    dS = -beta / N * I * S
    dI =  beta / N * I * S - gamma * I
    dR =  gamma * I
    return np.array([ dS, dI, dR ])


# Define IVP parameters
tspan = [0, 50]           # boundaries of the t domain
y0 = [99, 1, 0]           # initial values [S, I, R]
beta, gamma = 0.5, 0.1    # SIR model parameters
h = 1                     # step length

# Solve the IVP using the Euler method
t, y = euler(SIR, tspan, y0, h)

# Plot solution
fig, ax = plt.subplots()
plt.plot(t, y[:,0], "b-", label="Susceptible")
plt.plot(t, y[:,1], "r-", label="Infected")
plt.plot(t, y[:,2], "g-", label="Recovered")
plt.xlabel("time (days)", fontsize=12)
plt.ylabel("Population", fontsize=12)
plt.legend()
plt.show()

% Define IVP parameters
tspan = [0, 50];    % boundaries of the t domain
y0 = [99, 1, 0];    % initial values [S, I, R]
beta = 0.5;         % infection rate
gamma = 0.1;        % recovery rate
h = 1;              % step length

% Solve the IVP using the Euler method
[t, y] = euler(@(t,y)SIR(t, y, beta, gamma), tspan, y0, h);

% Plot solution
plot(t, y(:, 1), 'b-', LineWidth=2)
hold on
plot(t, y(:, 2), 'r-', LineWidth=2)
plot(t, y(:, 3), 'g-', LineWidth=2)
hold off
xlabel('$t$', Fontsize=14, Interpreter='latex')
ylabel('$y$', Fontsize=14, Interpreter='latex')
legend('Susceptible', 'Infected', 'Recovered', Location="east")
axis padded

% ---------------------------------------------------------------
function [t, y] = euler(f, tspan, y0, h)

nsteps = floor((tspan(2) - tspan(1)) / h);
t = zeros(nsteps + 1, 1);
y = zeros(nsteps + 1, length(y0));
y(1, :) = y0;

for n = 1 : length(t) - 1
    y(n+1, :) = y(n, :) + h * f(t(n), y(n, :));
    t(n+1, :) = t(n) + h;
end

end

function y = SIR(~, y, beta, gamma)

S = y(1); 
I = y(2);
R = y(3);
N = S + I + R;
y(1) = -beta / N * I * S;
y(2) =  beta / N * I * S - gamma * I;
y(3) = gamma * I;

end

Note

Note that the SIR model has been defined using a non-autonomous function so is placed at the bottom of the script file. The euler() function takes in 2 inputs t and y, so the addition input parameters beta and gamma are passed in using @(t, y)SIR(t, y, beta, gamma).