Explicit Runge-Kutta methods exercise solutions#
Solutions to the exercises on explicit Runge-Kutta methods.
Solution to Exercise 2.1
\[\begin{align*}
\begin{array}{c|cccc}
0 & 0 \\
1/4 & 1/4 \\
1/2 & 0 & 1/2 \\
1 & 1 & -2 & 2 \\ \hline
& 1/6 & 0 & 2/3 & 1/6
\end{array}
\end{align*}\]
Solution to Exercise 2.2
\[\begin{align*}
y_{n+1} &= y_n + \frac{h}{9}(4k_2 + 3k_3 + 2k_4), \\
k_1 &= f(t_n, y_n), \\
k_2 &= f(t_n + \frac{1}{4}h, y_n + \frac{1}{4} h k_1), \\
k_3 &= f(t_n + \frac{1}{2}h, y_n + h ( - \frac{1}{2}k_1 + k_2)), \\
k_4 &= f(t_n + h, y_n + h ( \frac{1}{4}k_1 + \frac{3}{4}k_3)).
\end{align*}\]
Solution to Exercise 2.3
The order conditions are:
\[\begin{align*}
\frac{1}{3} + b_2 &=1,\\
c_2 b_2 &=\frac{1}{2},\\
a_{21} &= c_2.
\end{align*}\]
Solving gives \(b_2 = \frac{2}{3}\), \(c_2=\frac{3}{4}\) and \(a_{21} = \frac{3}{4}\) so the method is
\[\begin{align*}
y_{n+1} &= y_n + \frac{h}{3}(k_1 + 2k_2), \\
k_1 &= f(t_n, y_n), \\
k_2 &= f(t_n + \frac{3}{4}h, y_n + \frac{3}{4}h k_1).
\end{align*}\]
Alternatively as a Butcher tableau
\[\begin{align*}
\begin{array}{c|cc}
0 & 0 \\
3/4 & 3/4 & 0 \\ \hline
& 1/3 & 2/3
\end{array}
\end{align*}\]
from sympy import *
# Declare symbolic variables
a21, b1, b2, c2 = symbols('a21, b1, b2, c2')
b1 = Rational(1,3)
# Define order conditions
eq1 = b1 + b2 - 1
eq2 = b2 * c2 - Rational(1,2)
eq3 = a21 * b2 - Rational(1,2)
# Solve order conditions
solve((eq1, eq2, eq3))
% Declare symbolic variables
syms a21 b1 b2 c2
b1 = 1 / 3;
% Define order conditions
eq1 = b1 + b2 == 1;
eq2 = b2 * c2 == 1 / 2;
eq3 = a21 == c2;
% Solve order conditions
solve(eq1, eq2, eq3)
Solution to Exercise 2.4
Adding the labels to the tree
\[\begin{split} \begin{align*}
r &= 10, \\
\Phi &= \sum_{i,j,k,\ell} b_i a_{ij} a_{ik} a_{k\ell} c_j^3 c_k c_\ell^2, \\
\gamma &= 10 \cdot 4 \cdot 5 \cdot 3 = 600.
\end{align*} \end{split}\]
Solution to Exercise 2.5
The set of rooted trees up to and including order 3 are
Tree |
\(\Phi\) |
\(\gamma\) |
|---|---|---|
|
\(\displaystyle\sum_i b_i\) |
1 |
|
\(\displaystyle\sum_i b_ic_i\) |
2 |
|
\(\displaystyle\sum_i b_ic_i^2\) |
3 |
|
\(\displaystyle\sum_{i,j} b_i a_{ij} c_j\) |
6 |
Using \(\Phi = \dfrac{1}{\gamma}\) we have
\[\begin{split} \begin{align*}
b_1 + b_2 + b_3 &= 1, \\
\textcolor{red}{b_1 c_1} + b_2 c_2 + b_3 c_3 &= \frac{1}{2}, \\
\textcolor{red}{b_1 c_1^2} + b_2 c_2^2 + b_3 c_3^2 &= \frac{1}{3}, \\
\textcolor{red}{b_1 a_{11} c_1} + \textcolor{red}{b_1 a_{12} c_2} + \textcolor{red}{b_1 a_{13} c_3} \quad & \\
\textcolor{red}{b_2 a_{21} c_1} + \textcolor{red}{b_2 a_{22} c_2} + \textcolor{red}{b_2 a_{23} c_3} \quad & \\
\textcolor{red}{b_3 a_{31} c_1} + b_3 a_{32} c_2 + \textcolor{red}{b_3 a_{33} c_3} &= \frac{1}{6}.
\end{align*} \end{split}\]
Since for an ERK method \(c_1 = 0\) and \(a_{ij} = 0\) where \(i \leq j\) then the terms in red are zero so the order conditions are (including the row sum conditions)
\[\begin{split} \begin{align*}
b_1 + b_2 + b_3 &= 1, \\
b_2 c_2 + b_3 c_3 &= \frac{1}{2}, \\
b_2 c_2^3 + b_3 c_3^2 &= \frac{1}{3}, \\
b_3 a_{32} c_2 &= \frac{1}{6}, \\
a_{21} &= c_2, \\
a_{31} + a_{32} &= c_3.
\end{align*} \end{split}\]
Solution to Exercise 2.6
Use Python or MATLAB to solve the order conditions
import sympy as sp
# Declare symbolic variables
a21, a31, a32, a41, a42, a43, b1, b2, b3, b4 = sp.symbols("a21, a31, a32, a41, a42, a43, b1, b2, b3, b4")
# Define c values
c2, c3, c4 = sp.Rational(1,4), sp.Rational(1,2), 1
# Define order conditions
eq1 = b1 + b2 + b3 + b4 - 1
eq2 = b2 * c2 + b3 * c3 + b4 * c4 - sp.Rational(1,2)
eq3 = b2 * c2 ** 2 + b3 * c3 ** 2 + b4 * c4 ** 2 - sp.Rational(1,3)
eq4 = b2 * c2 ** 3 + b3 * c3 ** 3 + b4 * c4 ** 3 - sp.Rational(1,4)
eq5 = b3 * a32 * c2 + b4 * a42 * c2 + b4 * a43 * c3 - sp.Rational(1,6)
eq6 = b3 * a32 * c3 * c2 + b4 * c4 * a42 * c2 + b4 * c4 * a43 * c3 - sp.Rational(1,8)
eq7 = b3 * a32 * c2 ** 2 + b4 * a42 * c2 ** 2 + b4 * a43 * c3 ** 2 - sp.Rational(1,12)
eq8 = c2 - a21
eq9 = c3 - a31 - a32
eq10 = c4 - a41 - a42 - a43
# Solve the order conditions
sp.solve((eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9, eq10))
% Declare symbolic variables
syms a21 a31 a32 a41 a42 a43 b1 b2 b3 b4
% Define c values
c2 = 1/4;
c3 = 1/2;
c4 = 1;
% Define order conditions
eq1 = b1 + b2 + b3 + b4 == 1;
eq2 = b2 * c2 + b3 * c3 + b4 * c4 == 1/2;
eq3 = b2 * c2^2 + b3 * c3^2 + b4 * c4^2 == 1/3;
eq4 = b2 * c2^3 + b3 * c3^3 + b4 * c4^3 == 1/4;
eq5 = b3 * a32 * c2 + b4 * a42 * c2 + b4 * a43 * c3 == 1/6;
eq6 = b3 * a32 * c3 * c2 + b4 * c4 * a42 * c2 + b4 * c4 * a43 * c3 == 1/8;
eq7 = b3 * a32 * c2^2 + b4 * a42 * c2^2 + b4 * a43 * c3^2 == 1/12;
eq8 = c2 - a21;
eq9 = c3 - a31 - a32;
eq10 = c4 - a41 - a42 - a43;
% Solve order conditions
solve(eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9, eq10)
Output:
{a31: 0,
a32: 1/2,
a41: 1,
a42: -2,
a43: 2,
b1: 1/6,
b2: 0,
b3: 2/3,
b4: 1/6,
a21: 1/4}
The Butcher tableau for this method is
\[\begin{split} \begin{align*}
\begin{array}{c|cccc}
0 & \\
1/4 & 1/4 \\
1/2 & 0 & 1/2 \\
1 & 1 & -2 & 2 \\ \hline
& 1/6 & 0 & 2/3 & 1/6
\end{array}
\end{align*} \end{split}\]
Solution to Exercise 2.7
The \(t_n\) values are
\[\begin{split} \vec{t} = \begin{pmatrix} 0.0 \\ 0.4 \\ 0.8 \\ 1.2 \\ 1.6 \\ 2.0 \end{pmatrix}. \end{split}\]
Using the second-order ERK method derived in Exercise 2.3
\[\begin{split} \begin{align*}
y_0 &= 1, \\
k_1 &= f(t_0, y_0) = (0.0) - (1.0) = -1, \\
k_2 &= f(t_0 + \tfrac{3}{4}h, y_0 + \tfrac{3}{4}hk_1) \\
&= (0 + \tfrac{3}{4}(0.4)) - (1 + \tfrac{3}{4}(0.4)(-1)) \\
&= -0.4, \\
y_1 &= y_0 + \frac{h}{3}(k_1 + k_2) \\
&= 1 + \frac{0.4}{3}(-1 + 2(-0.4)) \\
&= 0.76,\\ \\
k_1 &= f(t_1, y_1) = (0.4) - (0.76) = -0.36, \\
k_2 &= f(t_1 + \tfrac{3}{4}h, y_1 + \tfrac{3}{4}hk_1) \\
&= (0.4 + \tfrac{3}{4}(0.4)) - (0.76 + \tfrac{3}{4}(0.4)(-0.36)) \\
&= 0.048, \\
y_2 &= y_1 + \frac{h}{3}(k_1 + k_2) \\
&= 0.76 + \frac{0.4}{3}(-0.36 + 2(0.048)) \\
&= 0.7248,\\ \\
k_1 &= f(t_2, y_2) = (0.8) - (0.7248) = 0.0752, \\
k_2 &= f(t_2 + \tfrac{3}{4}h, y_2 + \tfrac{3}{4}hk_1) \\
&= (0.8 + \tfrac{3}{4}(0.4)) - (0.7248 + \tfrac{3}{4}(0.4)(0.0752)) \\
&= 0.3526, \\
y_3 &= y_2 + \frac{h}{3}(k_1 + k_2) \\
&= 0.7248 + \frac{0.4}{3}(0.0752 + 2(0.3526)) \\
&= 0.8289,\\ \\
k_1 &= f(t_3, y_3) = (1.2) - (0.8289) = 0.3711, \\
k_2 &= f(t_3 + \tfrac{3}{4}h, y_3 + \tfrac{3}{4}hk_1) \\
&= (1.2 + \tfrac{3}{4}(0.4)) - (0.8289 + \tfrac{3}{4}(0.4)(0.3711)) \\
&= 0.5598, \\
y_4 &= y_3 + \frac{h}{3}(k_1 + k_2) \\
&= 0.8289 + \frac{0.4}{3}(0.3711 + 2(0.5598)) \\
&= 1.028,\\ \\
k_1 &= f(t_4, y_4) = (1.6) - (1.028) = 0.5724, \\
k_2 &= f(t_4 + \tfrac{3}{4}h, y_4 + \tfrac{3}{4}hk_1) \\
&= (1.6 + \tfrac{3}{4}(0.4)) - (1.028 + \tfrac{3}{4}(0.4)(0.5724)) \\
&= 0.7007, \\
y_5 &= y_4 + \frac{h}{3}(k_1 + k_2) \\
&= 1.028 + \frac{0.4}{3}(0.5724 + 2(0.7007)) \\
&= 1.291,\\ \\
\end{align*} \end{split}\]
So the solution is
\[\begin{split} \begin{align*}
\vec{y} &=
\begin{pmatrix}
1 \\
0.76 \\
0.7248 \\
0.8289 \\
1.0276 \\
1.2908
\end{pmatrix}.
\end{align*} \end{split}\]
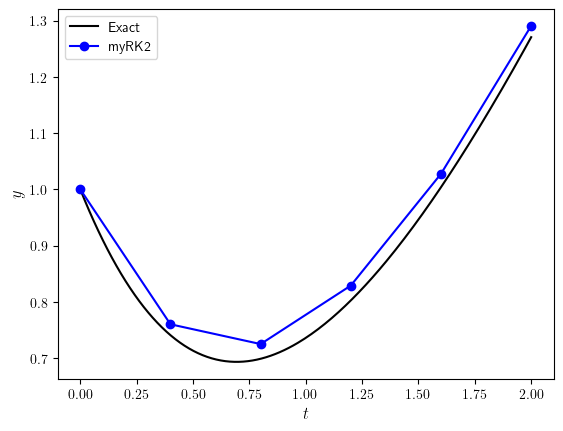
Solution to Exercise 2.8
Solution
| t | y | Exact |
|:----:|:---------:|:---------:|
| 0.00 | 1.000000 | 1.000000 |
| 0.40 | 0.760000 | 0.740640 |
| 0.80 | 0.724800 | 0.698658 |
| 1.20 | 0.828864 | 0.802388 |
| 1.60 | 1.027628 | 1.003793 |
| 2.00 | 1.290787 | 1.270671 |
Plot
Code
import numpy as np
import matplotlib.pyplot as plt
def myrk2(f, t, y, h):
k1 = f(t, y)
k2 = f(t + 3/4 * h, y + 3 / 4 * h * k1)
return y + h / 3 * (k1 + 2 * k2)
def solveIVP(f, tspan, y0, h, solver):
# Initialise t and y arrays
t = np.arange(tspan[0], tspan[1] + h, h)
y = np.zeros((len(t),len(y0)))
t[0] = tspan[0]
y[0,:] = y0
# Loop through steps and calculate single step solver solution
for n in range(len(t) - 1):
y[n+1,:] = solver(f, t[n], y[n,:], h)
return t, y
# Define ODE function and exact solution
def f(t, y):
return t - y
def exact(t):
return t + 2 * np.exp(-t) - 1
# Define IVP
tspan = [0, 2] # boundaries of the t domain
y0 = [1] # solution at the lower boundary
h = 0.4 # step length
# Calculate the solution to the IVP
t, y = solveIVP(f, tspan, y0, h, myrk2)
# Print table of solution values
print("| t | y | Exact |")
print("|:----:|:---------:|:---------:|")
for n in range(len(t)):
print(f"| {t[n]:4.2f} | {y[n,0]:9.6f} | {exact(t[n]):9.6f} |")
# Plot solutions
t_exact = np.linspace(tspan[0], tspan[1], 200)
y_exact = exact(t_exact)
fig, ax = plt.subplots()
plt.plot(t_exact, y_exact, "k", label="Exact")
plt.plot(t, y, "bo-", label="myRK2")
plt.xlabel("$t$", fontsize=12)
plt.ylabel("$y$", fontsize=12)
plt.legend()
plt.show()
% Define ODE function and exact solution
f = @(t, y) t - y;
exact = @(t) t + 2 * exp(-t) - 1;
% Define IVP parameters
tspan = [0, 2]; % boundaries of the t domain
y0 = 1; % initial value of the solution
h = 0.4; % step length
% Calculate the solution to the IVP
[t, y_myrk2] = solveIVP(f, tspan, y0, h, @myrk2);
% Calculate exact solution for plotting
texact = linspace(tspan(1), tspan(2), 200);
yexact = exact(texact);
% Print table of solution values (for loop is used to group print statements)
for i = 1 : 1
fprintf('| t | y | Exact |\n|:----:|:---------:|:---------:|');
for n = 1 : length(t)
fprintf('\n| %4.2f | %9.6f | %9.6f |', t(n), y_myrk2(n), exact(t(n)));
end
end
% Plot solution
plot(texact, yexact, 'k-', LineWidth=2)
hold on
plot(t, y_myrk2, 'b-o', LineWidth=2, MarkerFaceColor='b')
hold off
axis padded
xlabel('$t$', FontSize=14, Interpreter='latex')
ylabel('$y$', FontSize=14, Interpreter='latex')
legend('Exact', 'myRK2', Location='northwest', FontSize=12)
% ----------------------------------------------------------------------------
function [t, y] = solveIVP(f, tspan, y0, h, solver)
% Define t and y arrays
t = (tspan(1) : h : tspan(2));
y = zeros(length(t), length(y0));
y(1,:) = y0;
% Loop through the steps and calculate single step solver solution
for n = 1 : length(t) - 1
y(n+1,:) = solver(f, t(n), y(n,:), h);
end
end
% ----------------------------------------------------------------------------
function ynew = myrk2(f, t, y, h)
k1 = f(t, y);
k2 = f(t + 3/4 * h, y + 3/4 * h * k1);
ynew = y + h / 3 * (k1 + 2 * k2);
end
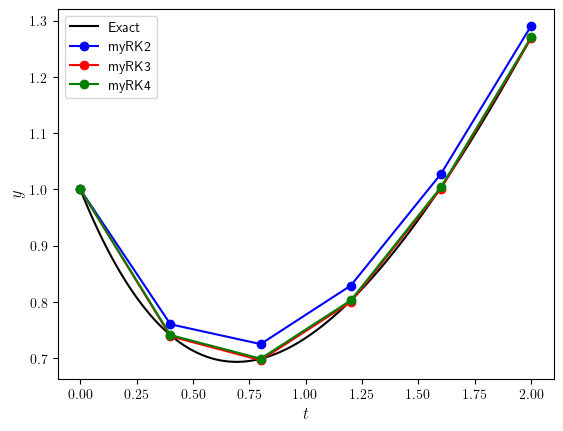
Solution to Exercise 2.9
Plot
Code
import numpy as np
import matplotlib.pyplot as plt
def myrk2(f, t, y, h):
k1 = f(t, y)
k2 = f(t + 3/4 * h, y + 3 / 4 * h * k1)
return y + h / 3 * (k1 + 2 * k2)
def myrk3(f, t, y, h):
k1 = f(t, y)
k2 = f(t + 1/2 * h, y + 1/2 * h * k1)
k3 = f(t + h, y + h * (-k1 + 2 * k2))
return y + h / 6 * (k1 + 4 * k2 + k3)
def myrk4(f, t, y, h):
k1 = f(t, y)
k2 = f(t + 1/4 * h, y + 1/4 * h * k1)
k3 = f(t + 1/2 * h, y + 1/2 * h * k2)
k4 = f(t + h, y + h * (k1 - 2 * k2 + 2 * k3))
return y + h / 6 * (k1 + 4 * k3 + k4)
def solveIVP(f, tspan, y0, h, solver):
# Initialise t and y arrays
t = np.arange(tspan[0], tspan[1] + h, h)
y = np.zeros((len(t),len(y0)))
t[0] = tspan[0]
y[0,:] = y0
# Loop through steps and calculate single step solver solution
for n in range(len(t) - 1):
y[n+1,:] = solver(f, t[n], y[n,:], h)
return t, y
# Define ODE function and exact solution
def f(t, y):
return t - y
def exact(t):
return t + 2 * np.exp(-t) - 1
# Define IVP
tspan = [0, 2] # boundaries of the t domain
y0 = [1] # solution at the lower boundary
h = 0.4 # step length
# Calculate the solution to the IVP
t, y_myrk2 = solveIVP(f, tspan, y0, h, myrk2)
t, y_myrk3 = solveIVP(f, tspan, y0, h, myrk3)
t, y_myrk4 = solveIVP(f, tspan, y0, h, myrk4)
# Plot solutions
t_exact = np.linspace(tspan[0], tspan[1], 200)
y_exact = exact(t_exact)
fig, ax = plt.subplots()
plt.plot(t_exact, y_exact, "k", label="Exact")
plt.plot(t, y_myrk2, "bo-", label="myRK2")
plt.plot(t, y_myrk3, "ro-", label="myRK3")
plt.plot(t, y_myrk4, "go-", label="myRK4")
plt.xlabel("$t$", fontsize=12)
plt.ylabel("$y$", fontsize=12)
plt.legend()
plt.show()
% Define ODE function and exact solution
f = @(t, y) t - y;
exact = @(t) t + 2 * exp(-t) - 1;
% Define IVP parameters
tspan = [0, 2]; % boundaries of the t domain
y0 = 1; % initial value of the solution
h = 0.4; % step length
% Calculate the solution to the IVP
[t, y_myrk2] = solveIVP(f, tspan, y0, h, @myrk2);
[t, y_myrk3] = solveIVP(f, tspan, y0, h, @myrk3);
[t, y_myrk4] = solveIVP(f, tspan, y0, h, @myrk4);
% Calculate exact solution for plotting
texact = linspace(tspan(1), tspan(2), 200);
yexact = exact(texact);
% Plot solution
plot(texact, yexact, 'k-', LineWidth=1)
hold on
plot(t, y_myrk2, 'b-o', LineWidth=2, MarkerFaceColor='b')
plot(t, y_myrk3, 'r-o', LineWidth=2, MarkerFaceColor='r')
plot(t, y_myrk4, 'g-o', LineWidth=2, MarkerFaceColor='g')
hold off
axis padded
xlabel('$t$', FontSize=14, Interpreter='latex')
ylabel('$y$', FontSize=14, Interpreter='latex')
legend('Exact', 'myRK2', 'myRK3', 'myRK4', Location='northwest', FontSize=12)
% ----------------------------------------------------------------------------
function [t, y] = solveIVP(f, tspan, y0, h, solver)
% Define t and y arrays
t = (tspan(1) : h : tspan(2));
y = zeros(length(t), length(y0));
y(1,:) = y0;
% Loop through the steps and calculate single step solver solution
for n = 1 : length(t) - 1
y(n+1,:) = solver(f, t(n), y(n,:), h);
end
end
% ----------------------------------------------------------------------------
function ynew = myrk2(f, t, y, h)
k1 = f(t, y);
k2 = f(t + 3/4 * h, y + 3/4 * h * k1);
ynew = y + h / 3 * (k1 + 2 * k2);
end
% ----------------------------------------------------------------------------
function ynew = myrk3(f, t, y, h)
k1 = f(t, y);
k2 = f(t + 1/2 * h, y + 1/2 * h * k1);
k3 = f(t + h, y + h * (-k1 + 2 * k2));
ynew = y + h / 6 * (k1 + 4 * k2 + k3);
end
% ----------------------------------------------------------------------------
function ynew = myrk4(f, t, y, h)
k1 = f(t, y);
k2 = f(t + 1/4 * h, y + 1/4 * h * k1);
k3 = f(t + 1/2 * h, y + 1/2 * h * k2);
k4 = f(t + h, y + h * (k1 - 2 * k2 + 2 * k3));
ynew = y + h / 6 * (k1 + 4 * k3 + k4);
end
Solution to Exercise 2.10
Global truncation errors
| h | myRK2 | myRK3 | myRK4 |
|:-----:|:--------:|:--------:|:--------:|
| 0.400 | 2.01e-02 | 1.99e-03 | 1.61e-04 |
| 0.200 | 4.23e-03 | 2.12e-04 | 8.53e-06 |
| 0.100 | 9.74e-04 | 2.44e-05 | 4.90e-07 |
| 0.050 | 2.34e-04 | 2.93e-06 | 2.94e-08 |
| 0.025 | 5.75e-05 | 3.60e-07 | 1.80e-09 |
Plot
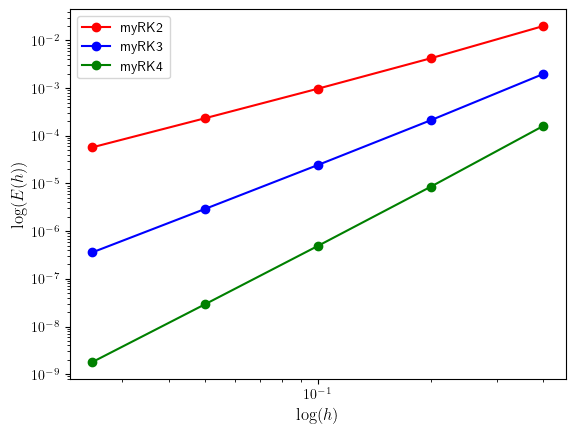
Estimating the order of the methods
\[\begin{split} \begin{align*}
\text{myRK2}: && n & \approx \frac{\log(2.01 \times 10^{-2}) - \log(5.75 \times 10^{-5})}{\log(0.4) - \log(0.025)} = 2.11 \approx 2, \\
\text{myRK3}: && n & \approx \frac{\log(1.99 \times 10^{-3}) - \log(8.53 \times 10^{-6})}{\log(0.4) - \log(0.025)} = 3.11 \approx 3, \\
\text{myRK4}: && n & \approx \frac{\log(1.61 \times 10^{-4}) - \log(1.80 \times 10^{-9})}{\log(0.4) - \log(0.025)} = 4.11 \approx 4.
\end{align*} \end{split}\]
Code
# Calculate solution for decreasing step lengths
hvals = [0.4, 0.2, 0.1, 0.05, 0.025]
tval = 2
E_myrk2, E_myrk3, E_myrk4 = [], [], []
for h in hvals:
t, y_myrk2 = solveIVP(f, tspan, y0, h, myrk2)
t, y_myrk3 = solveIVP(f, tspan, y0, h, myrk3)
t, y_myrk4 = solveIVP(f, tspan, y0, h, myrk4)
idx = np.argmin(abs(t - tval))
E_myrk2.append(abs(exact(tval) - y_myrk2[idx,0]))
E_myrk3.append(abs(exact(tval) - y_myrk3[idx,0]))
E_myrk4.append(abs(exact(tval) - y_myrk4[idx,0]))
# Output table of errors
print("| h | myRK2 | myRK3 | myRK4 |")
print("|:-----:|:--------:|:--------:|:--------:|")
for n in range(len(hvals)):
print(f"| {hvals[n]:0.3f} | {E_myrk2[n]:0.2e} | {E_myrk3[n]:0.2e} | {E_myrk4[n]:0.2e} |")
# Plot errors on a log scale
fig, ax = plt.subplots()
plt.loglog(hvals, E_myrk2, 'ro-', label="myRK2")
plt.loglog(hvals, E_myrk3, 'bo-', label="myRK3")
plt.loglog(hvals, E_myrk4, 'go-', label="myRK4")
plt.xlabel(r"$\log(h)$", fontsize=12)
plt.ylabel(r"$\log(E(h))$", fontsize=12)
plt.legend()
plt.show()
% Calculate solution for decreasing step lengths
hvals = [0.4, 0.2, 0.1, 0.05, 0.025];
tval = 2;
E_myrk2 = [];
E_myrk3 = [];
E_myrk4 = [];
for h = hvals
[t, y_myrk2] = solveIVP(f, tspan, y0, h, @myrk2);
[t, y_myrk3] = solveIVP(f, tspan, y0, h, @myrk3);
[t, y_myrk4] = solveIVP(f, tspan, y0, h, @myrk4);
[~, idx] = min(abs(tval - t));
E_myrk2 = [E_myrk2, abs(exact(tval) - y_myrk2(idx))];
E_myrk3 = [E_myrk3, abs(exact(tval) - y_myrk3(idx))];
E_myrk4 = [E_myrk4, abs(exact(tval) - y_myrk4(idx))];
end
% Output table of errors (for loop is used to group print statements)
for i = 1 : 1
fprintf('| t | myRK2 | myRK4 | myRK4 |')
fprintf('|:-----:|:--------:|:--------:|:--------:|');
for n = 1 : length(hvals)
fprintf('\n| %1.3f | %1.2e | %1.2e | %1.2e |', hvals(n), E_myrk2(n), E_myrk3(n), E_myrk4(n))
end
end
% Plot errors on a loglog scale
loglog(hvals, E_myrk2, 'ro-', MarkerFaceColor='r', LineWidth=2)
hold on
loglog(hvals, E_myrk3, 'bo-', MarkerFaceColor='b', LineWidth=2)
loglog(hvals, E_myrk4, 'go-', MarkerFaceColor='g', LineWidth=2)
hold off
axis padded
xlabel('$\log(h)$', FontSize=14, Interpreter='latex')
ylabel('$\log(E(h))$', FontSize=14, Interpreter='latex')
legend('myRK2', 'myRK3', 'myRK4', Location='southeast', FontSize=12)
Solution to Exercise 2.11
Plot
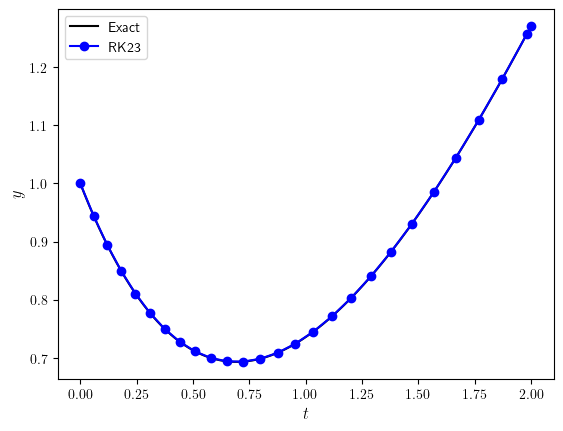
There were 26 successful steps and 3 failed steps.
Code
import numpy as np
import matplotlib.pyplot as plt
def solveIVP_SSC(f, tspan, y0, h, solver, tol=1e-4):
# Define t and y arrays
t = np.zeros(10000)
y = np.zeros((10000,len(y0)))
t[0] = tspan[0]
y[0,:] = y0
# Solver loop
n = 0
while t[n] < tspan[-1]:
# Ensure t does not exceed tmax
h = min(h, tspan[-1] - t[n])
# Calculate order p+1 and p solutions
yp1, yp, order = solver(f, t[n], y[n,:], h)
# Determine whether step was successful or not
delta = np.max(np.abs(yp1 - yp))
if delta < tol:
y[n+1,:] = yp1
t[n+1] = t[n] + h
n += 1
# Calculate new value of h
h *= max(0.5, min(2, 0.9 * (tol / delta) ** (1 / (order + 1))))
return t[:n+1], y[:n+1,:]
def rk23(f, t, y, h):
k1 = f(t, y)
k2 = f(t + 1/2 * h, y + 1/2 * h * k1)
k3 = f(t + h, y + h * (-k1 + 2 * k2))
y3 = y + h / 6 * (k1 + 4 * k2 + k3)
y2 = y + h * k2
return y3, y2, 2
# Define ODE function and exact solution
def f(t, y):
return t - y
def exact(t):
return t + 2 * np.exp(-t) - 1
# Define IVP
tspan = [0, 2] # boundaries of the t domain
y0 = [1] # solution at the lower boundary
h = 0.4 # step length
tol = 1e-4 # accuracy tolerance
# Calculate the solution to the IVP
t, y = solveIVP_SSC(f, tspan, y0, h, rk23, tol)
# Plot solutions
t_exact = np.linspace(tspan[0], tspan[1], 200)
y_exact = exact(t_exact)
fig, ax = plt.subplots()
plt.plot(t_exact, y_exact, "k", label="Exact")
plt.plot(t, y, "bo-", label="RK23")
plt.xlabel("$t$", fontsize=12)
plt.ylabel("$y$", fontsize=12)
plt.legend()
plt.show()
% Define ODE function and exact solution
f = @(t, y) t - y;
exact = @(t) t + 2 * exp(-t) - 1;
% Define IVP parameters
tspan = [0, 2]; % boundaries of the t domain
y0 = 1; % initial value of the solution
h0 = 0.4; % step length
tol = 1e-4; % accuracy tolerance
% Calculate the solution to the IVP
[t, y] = solveIVP_SSC(f, tspan, y0, h0, @rk23, tol);
% Output number of successful steps
fprintf("%0i successful steps", length(t) - 1)
% Calculate exact solution for plotting
texact = linspace(tspan(1), tspan(2), 200);
yexact = exact(texact);
% Plot solution
plot(texact, yexact, 'k-', LineWidth=2)
hold on
plot(t, y, 'b-o', LineWidth=2, MarkerFaceColor='b')
hold off
axis padded
xlabel('$t$', FontSize=14, Interpreter='latex')
ylabel('$y$', FontSize=14, Interpreter='latex')
legend('Exact', 'myRK2', Location='northwest', FontSize=12)
% ----------------------------------------------------------------------------
function [t, y] = solveIVP_SSC(f, tspan, y0, h, solver, tol)
% Define t and y arrays
t = zeros(10000);
y = zeros(10000, length(y0));
t(1) = tspan(1);
y(1,:) = y0;
% Loop through the steps
n = 1;
while t(n) < tspan(2)
% Ensure t does not exceed tmax
h = min(h, tspan(2) - t(n));
% Calculate order p and p+1 solutions
[yp1, yp, p] = solver(f, t(n), y(n,:), h);
% Determine whether the step was successful or not
delta = max(abs(yp1 - yp));
if delta < tol
y(n+1,:) = yp1;
t(n+1) = t(n) + h;
n = n + 1;
end
% Calculate new value of h
h = h * max(0.5, min(2, 0.9 * (tol / delta) ^ (1 / (p + 1))));
end
% Remove unused entries from t and y
t(n+1:end) = [];
y(n+1:end,:) = [];
% Print number of successful and failed steps
fprintf("%1i successful steps\n%1i failed steps", nsucc, nfail)
end
% ----------------------------------------------------------------------------
function [y3, y2, order] = rk23(f, t, y, h)
k1 = f(t, y);
k2 = f(t + 1/2 * h, y + 1/2 * h * k1);
k3 = f(t + h, y + h * (-k1 + 2 * k2));
y3 = y + h * (1/6 * k1 + 2/3 * k2 + 1/6 * k3);
y2 = y + h * k2;
order = 2
end