Implicit Runge-Kutta methods exercise solutions

Implicit Runge-Kutta methods exercise solutions#

Solutions to the exercises on implicit Runge-Kutta methods.

Checking the \(B(k)\) condition

\[\begin{split} \begin{align*} B(1) &= b_1 + b_2 = \frac{1}{2} + \frac{1}{2} = 1, \\ B(2) &= b_1c_1 + b_2c_2 = \frac{1}{2} \left(\frac{1}{4}\right) + \frac{1}{2}\left(\frac{3}{4}\right) = \frac{1}{2}, \\ B(3) &= b_1c_1^2 + b_2c_2^2 = \frac{1}{2} \left(\frac{1}{16}\right) + \frac{1}{2}\left(\frac{9}{16}\right) = \frac{5}{16}, \end{align*} \end{split}\]

so the \(B(k)\) condition is satisfied up to \(k=2\). Checking the \(C(1)\) condition

\[\begin{split} \begin{align*} \ell &= 1, & i &= 1: & LHS &= a_{11} + a_{12} = \frac{1}{4} + 0 = \frac{1}{4}, \\ &&&& RHS &= c_1 = \frac{1}{4}, \\ \ell &= 1, & i &= 2: & LHS &= a_{21} + a_{22} = \frac{1}{2} + \frac{1}{4} = \frac{3}{4}, \\ &&&& RHS &= c_2 = \frac{3}{4} \end{align*} \end{split}\]

so the \(C(1)\) condition is satisfied. Checking the \(D(1)\) condition

\[\begin{split} \begin{align*} \ell &= 1, & i &= 1: & LHS &= b_1a_{11} + b_2a_{21} = \frac{1}{2}\left(\frac{1}{4}\right) + \frac{1}{2}\left(\frac{1}{2}\right) = \frac{3}{8}, \\ &&&& RHS &= b_1(1 - c_1) = \frac{1}{2}\left(1 - \frac{1}{4}\right) = \frac{3}{8}, \\ \ell &= 1, & i &= 2: & LHS &= b_1a_{12} + b_2a_{22} = \frac{1}{2}(0) + \frac{1}{2}\left(\frac{1}{4}\right) = \frac{1}{8}, \\ &&&& RHS &= b_2(1 - c_2) = \frac{1}{2}\left(1 - \frac{3}{4}\right) = \frac{1}{8}. \end{align*} \end{split}\]

so the \(D(1)\) conditions is satisfied. Therefore this method is a second-order method.

Solution to Exercise 3.2

A third-order Radau IIA method has \(s=2\) stages with \(c_2 = 1\). The value of \(c_1\) is the other root of \(0 = P_2(t) - P_1(t)\) and the \(a_{ij}\) and \(b_i\) coefficients satisfy the \(B(3)\) and \(C(2)\) conditions respectively.

\[\begin{split} \begin{align*} b_1 + b_2 &= 1, \\ b_1c_1 + b_2 &= \frac{1}{2}, \\ b_1c_1^2 + b_2 &= \frac{1}{3}, \\ a_{11} + a_{12} &= c_1, \\ a_{21} + a_{22} &= 1, \\ a_{11}c_1 + a_{12} &= \frac{1}{2} c_1^2, \\ a_{21}c_1 + a_{22} &= \frac{1}{2}. \end{align*} \end{split}\]

Solving the order conditions using Python of MATLAB:

Python

import sympy as sp
  
# Define symbolic variables
a11, a12, a21, a22, b1, b2, c1, c2 = sp.symbols("a11, a12, a21, a22, b1, b2, c1, c2")

# Define Legendre polynomial
def P(n):
    Pn, x = 0, sp.symbols('x')
    for k in range(n + 1):
        Pn += sp.binomial(n, k) * sp.binomial(n + k, k) * (x - 1) ** k

    return Pn


# Calculate c values
c1, c2 = sp.solve(P(2) - P(1))
print(f"c1 = {c1}\nc2 = {c2}")

# Define order conditions
eq1 = b1 + b2 - 1
eq2 = b1 * c1 + b2 - sp.Rational(1,2)
eq3 = a11 + a12 - c1
eq4 = a11 + a12 - c1
eq5 = a21 + a22 - 1
eq6 = a11 * c1 + a12 - sp.Rational(1,2) * c1 ** 2
eq7 = a21 * c1 + a22 - sp.Rational(1,2)

# Solve order conditions
sp.solve((eq1, eq2, eq3, eq4, eq5, eq6, eq7))

MATLAB

syms a11 a12 a21 a22 b1 b2 c1 c2

% Calculate c coefficients
c = solve(P(2) - P(1))
c1 = c(1);
c2 = c(2);

% Define order conditions
eq1 = b1 + b2 == 1;
eq2 = b1 * c1 + b2 == 1/2;
eq3 = b1 * c1 ^ 2 + b2 == 1/3;
eq3 = a11 + a12 == c1;
eq4 = a21 + a22 == 1;
eq5 = a11 * c1 + a12 * c2 == 1/2 * c1^2;
eq6 = a21 * c1 + a22 * c2 == 1/2;

% Solve order conditions
solve(eq1, eq2, eq3, eq4, eq5, eq6, eq7)

% -------------------------------------------------------------------
function Pn = P(n)

syms x
Pn = 0;
for k = 0 : n
    Pn = Pn + nchoosek(n, k) * nchoosek(n + k, k) * (x - 1) ^ k;
end

end

Output:

c1 = 1/3
c2 = 1

{b1: 3/4, b2: 1/4, a11: 5/12, a12: -1/12, a21: 3/4, a22: 1/4}

So the third-order RadauIIA method is

\[\begin{split} \begin{array}{c|cc} 1/3 & 5/12 & -1/12 \\ 1 & 3/4 & 1/4 \\ \hline & 3/4 & 1/4 \end{array} \end{split}\]

Solution to Exercise 3.3

The Butcher tableau for the Radau IIA method is

\[\begin{align*} \begin{array}{c|cc} 1/3 & 5/12 & -1/12 \\ 1 & 3/4 & 1/4 \\ \hline & 3/4 & 1/4 \end{array} \end{align*}\]

The stage values are

\[\begin{align*} Y_1 &= y_n + h (\tfrac{5}{12} f(t_n + \tfrac{1}{3} h, Y_1) - \tfrac{1}{12} f(t_n + h, Y_2)) \\ Y_2 &= y_n + h (\tfrac{3}{4} f(t_n + \tfrac{1}{3} h, Y_1) + \tfrac{1}{4} f(t_n + h, Y_2)), \end{align*}\]

and since \(f(t,y) = t - y \) then

\[\begin{align*} Y_1 &= y_n + h (\tfrac{5}{12} (t_n + \tfrac{1}{3} h - Y_1) - \tfrac{1}{12} (t_n + h - Y_2)) \\ Y_2 &= y_n + h (\tfrac{3}{4} (t_n + \tfrac{1}{3} h - Y_1) + \tfrac{1}{4} (t_n + h - Y_2)). \end{align*}\]

For this problem \(y(0) = 1\) and \(h = 0.4\). Using starting estimates of \(Y_1 = Y_2 = 1\) the iteration values are

\(k\)	\(Y_1^{(k)}\)	\(Y_2^{(k)}\)	Max difference
0	1.000000	1.000000	-
1	0.875556	0.717333	2.83e-01
2	0.886874	0.742204	2.49e-02
3	0.885817	0.740035	2.17e-03
4	0.885921	0.740220	1.86e-04
5	0.885909	0.740205	1.52e-05

The solution over the first step is

\[\begin{align*} y_1 &= y_0 + h (\tfrac{3}{4} (t_0 + \tfrac{1}{3}(0.4) - Y_1) + \tfrac{1}{4} (t_0 + 0.4 - Y_2)), \\ &= 1 + 0.4 (\tfrac{3}{4} (0 + \tfrac{1}{3}(0.4) - 0.885909) + \tfrac{1}{4} (0 + 0.4 - 0.740205)), \\ &= 0.740207. \end{align*}\]

Solution to Exercise 3.4

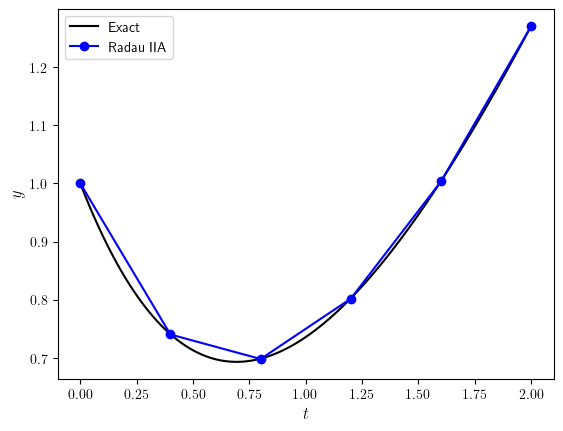
Table

|  t   |     y     |   Exact   |   Error  |
|:----:|:---------:|:---------:|:--------:|
| 0.00 |  1.000000 |  1.000000 | 0.00e+00 |
| 0.40 |  0.740207 |  0.740640 | 4.33e-04 |
| 0.80 |  0.698075 |  0.698658 | 5.83e-04 |
| 1.20 |  0.801801 |  0.802388 | 5.87e-04 |
| 1.60 |  1.003268 |  1.003793 | 5.25e-04 |
| 2.00 |  1.270232 |  1.270671 | 4.39e-04 |

Plot

../_images/fea2fdc9955919f588d0269e98a0bce966b5eef9d795116d856247dd51c2f3cc.png

Python

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['text.usetex'] = True  # allows use of LaTeX in labels

def solveIVP(f, tspan, y0, h, solver):

    # Initialise t and y arrays
    t = np.arange(tspan[0], tspan[1] + h, h)
    y = np.zeros((len(t),len(y0)))
    t[0] = tspan[0]
    y[0,:] = y0

    # Loop through steps and calculate single step solver solution
    for n in range(len(t) - 1):
        y[n+1,:] = solver(f, t[n], y[n,:], h)
              
    return t, y


def radauIIA(f, t, y, h): 

    # Calculate stage values
    Y1, Y2 = np.ones(len(y0)), np.ones(len(y0))
    Y1old, Y2old = np.ones(len(y0)), np.ones(len(y0))
    for k in range(10):
        Y1 = y + h * (5/12 * f(t + 1/3 * h, Y1) - 1/12 * f(t + h, Y2))
        Y2 = y + h * (3/4 * f(t + 1/3 * h, Y1) + 1/4 * f(t + h, Y2))

        if max(np.amax(abs(Y1 - Y1old)), np.amax(abs(Y2 - Y2old))) < 1e-4:
            break

        Y1old, Y2old = Y1, Y2

    return y + h / 4 * (3 * f(t + 1/3 * h, Y1) +  f(t + h,Y2))


# Define ODE function
def f(t, y):
    return t - y

def exact(t):
    return t + 2 * np.exp(-t) - 1


# Define IVP
tspan = [0, 2]  # boundaries of the t domain
y0 = [1]        # solution at the lower boundary
h = 0.4         # step length
tol = 1e-4      # convergence tolerance

# Solve IVP using the IRK method
t, y = solveIVP(f, tspan, y0, h, radauIIA)

# Print table of solution values
print("|  t   |     y     |   Exact   |   Error  |")
print("|:----:|:---------:|:---------:|:--------:|")
for n in range(len(t)):
    print(f"| {t[n]:4.2f} | {y[n,0]:9.6f} | {exact(t[n]):9.6f} | {abs(exact(t[n]) - y[n,0]):0.2e} |")

# Plot solutions
t_exact = np.linspace(tspan[0], tspan[1], 200)
y_exact = exact(t_exact)
fig, ax = plt.subplots()
plt.plot(t_exact, y_exact, "k", label="Exact")
plt.plot(t, y, "bo-", label="Radau IIA")
plt.xlabel("$t$", fontsize=12)
plt.ylabel("$y$", fontsize=12)
plt.legend()
plt.show()

MATLAB

% Define ODE function and exact solution
f = @(t, y) t - y;
exact = @(t) t + 2 * exp(-t) - 1;

% Define IVP parameters
tspan = [0, 2];     % boundaries of the t domain
y0 = 1;             % initial value of the solution
h = 0.4;            % step length
tol = 1e-4;         % accuracy tolerance

% Calculate the solution to the IVP
[t, y] = solveIVP(f, tspan, y0, h, @radauIIA);

% Calculate exact solution for plotting
texact = linspace(tspan(1), tspan(2), 200);
yexact = exact(texact);

% Plot solution
plot(texact, yexact, 'k-', LineWidth=2)
hold on
plot(t, y, 'b-o', LineWidth=2, MarkerFaceColor='b')
hold off
axis padded
xlabel('$t$', FontSize=14, Interpreter='latex')
ylabel('$y$', FontSize=14, Interpreter='latex')
legend('Exact', 'Radau IIA', Location='northwest', FontSize=12)

% --------------------------------------------------------------------
function [t, y] = solveIVP(f, tspan, y0, h, solver)

% Define t and y arrays
t = (tspan(1) : h : tspan(2));
y = zeros(length(t), length(y0));
y(1,:) = y0;

% Loop through the steps and calculate single step solver solution
for n = 1 : length(t) - 1
    y(n+1,:) = solver(f, t(n), y(n,:), h);
end

end

% --------------------------------------------------------------------
function ynew = radauIIA(f, t, y, h)

neq = length(y);
Y1 = ones(neq);
Y2 = ones(neq);
Y1old = ones(neq);
Y2old = ones(neq);
for k = 1 : 10
    Y1 = y + h * (5/12 * f(t + 1/3 * h, Y1) - 1/12 * f(t + h, Y2));
    Y2 = y + h * (3/4 * f(t + 1/3 * h, Y1) + 1/4 * f(t + h, Y2));
    if max(max(abs(Y1 - Y1old)), max(abs(Y2 - Y2old))) < 1e-4
        break
    end
    Y1old = Y1;
    Y2old = Y2;
end
ynew = y + h / 4 * (3 * f(t + 1/3 * h, Y1) + f(t + h, Y2));

end