Stability exercises solutions

Stability exercises solutions#

Solutions to the exercises on stability.

\[\begin{align*} \vec{b} A^0 \vec{e} &= \begin{pmatrix} -1 \\ 2/3 \\ -1/3 \\ 2/3 \\ 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = 1, \\ \vec{b} A^1 \vec{e} &= \begin{pmatrix} -1 \\ 2/3 \\ -1/3 \\ 2/3 \\ 1 \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 1/4 & 0 & 0 & 0 & 0 \\ 1/2 & 0 & 0 & 0 & 0 \\ 0 & 1/2 & 1/4 & 0 & 0 \\ 0 & 1/6 & -1/3 & 1/6 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = \frac{1}{2}, \\ \vec{b} A^2 \vec{e} &= \begin{pmatrix} -1 \\ 2/3 \\ -1/3 \\ 2/3 \\ 1 \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 1/4 & 0 & 0 & 0 & 0 \\ -1/8 & 1/12 & 1/24 & 0 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = \frac{1}{6}, \\ \vec{b} A^3 \vec{e} &= \begin{pmatrix} -1 \\ 2/3 \\ -1/3 \\ 2/3 \\ 1 \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 1/24 & 0 & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = \frac{1}{24}, \\ \vec{b} A^4 \vec{e} &= \begin{pmatrix} -1 \\ 2/3 \\ -1/3 \\ 2/3 \\ 1 \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = 0, \\ \end{align*}\]

So the stability function is \(R(z) = 1 + z + \frac{1}{2} z^2 + \frac{1}{6} z^3 + \frac{1}{24} z^4\)

Code

Python

from sympy import *

# Define ERK method
A = Matrix([[0, 0, 0, 0, 0], 
            [Rational(1,4), 0, 0, 0, 0], 
            [Rational(1,2), 0, 0, 0, 0], 
            [0, Rational(1,2), Rational(1,4), 0, 0], 
            [0, Rational(1,6), -Rational(1,3), Rational(1,6), 0]])
b = Matrix([[-1], [Rational(2,3)], [-Rational(1,3)], [Rational(2,3)], [1]])
e = ones(5, 1)

# Calculate coefficients
for k in range(1, len(b) + 1):
    print((b.T * A ** (k - 1) * e)[0])

MATLAB

% Define ERK method
A = [0, 0, 0, 0, 0 ; 
    1/4, 0, 0, 0, 0 ; 
    1/2, 0, 0, 0, 0 ;
    0, 1/2, 1/4, 0, 0 ;
    0, 1/6, -1/3, 1/6, 0];
b = [-1 ; 2/3 ; -1/3 ; 2/3 ; 1];
e = ones(5, 1);

% Calculate coefficients
for k = 1 : length(b)
    sym(b' * A ^ (k - 1) * e)
end

Solution to Exercise 4.2

\[\begin{align*} R(z) &= \frac{\det \left( \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - z \begin{pmatrix} 7/24 & -1/24 \\ 13/24 & 5/24 \end{pmatrix} + z \begin{pmatrix} 1/2 & 0 \\ 0 & 1/2 \end{pmatrix} \right)}{\det \left( \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - z \begin{pmatrix} 7/24 & -1/24 \\ 13/24 & 5/24 \end{pmatrix} \right)} \\ &= \frac{\det \begin{pmatrix} 1 + 5z/24 & z/24 \\ -13z/24 & 1 + 7z/24 \end{pmatrix}}{\det \begin{pmatrix} 1 - 7z/24 & z/24 \\ -13z/34 & 1 - 5z/24 \end{pmatrix}} = \frac{1 + \frac{1}{2} z + \frac{1}{12} z^2}{1 - \frac{1}{2} z + \frac{1}{12} z^2}. \end{align*}\]

Check the roots of \(Q(z)\)

\[\begin{align*} 0 &= 1 - \frac{1}{2} z + \frac{1}{12} z^2, \\ \therefore z &= \frac{\frac{1}{2} \pm \sqrt{-\frac{1}{3}}}{\frac{1}{6}} = 3 \pm \sqrt{3}i, \end{align*}\]

so the roots of \(Q(z)\) have positive real parts so the first condition for A-stability is satisfied.

Check that \(E(y) \geq 0\)

\[\begin{align*} E(y) &= \left( 1 - \frac{1}{2} i y - \frac{1}{12} y^2 \right) \left( 1 + \frac{1}{2} i y - \frac{1}{12} y^2 \right) \\ & \qquad - \left( 1 - \frac{1}{2} i y - \frac{1}{12} y^2 \right) \left( 1 + \frac{1}{2} i y - \frac{1}{12} y^2 \right) = 0 \end{align*}\]

so \(E(y) \geq 0\) and the second condition for A-stability is satisfied. Since both conditions are satisfied then this method is A-stable

Code

Python

import sympy as sp

# Define numerator and denominator functions
def P(z):
    return (I - z * A + z * ebT).det()

def Q(z):
    return (I - z * A).det()

# Define RK method
A = sp.Matrix([[sp.Rational(7,24), -sp.Rational(1,24)], [sp.Rational(13,24), sp.Rational(5,24)]])
ebT = sp.Matrix([[sp.Rational(1,2), 0], [0, sp.Rational(1,2)]])
I = sp.eye(2)

# Calculate R(z)
z, y = sp.symbols('z, y')
R = P(z) / Q(z)
print("R(z) = ")
display(R)

# Check roots of Q have positive real parts
print('roots of Q(z) = ')
display(sp.solve(Q(z)))

# Check E(y) >= 0
E = Q(1j * y) * Q(-1j * y) - P(1j * y) * P(-1j * y)
print('E(y) = ')
display(sp.simplify(sp.nsimplify(E)))

MATLAB

% Define IRK method
A = [7/24, -1/24 ; 13/24, 5/24];
ebT = [1/2, 0 ; 0, 1/2];
I = eye(2);

% Calculate R(z)
syms z y

P = @(z) det(I - z * A + z * ebT);
Q = @(z) det(I - z * A);

Rz = P(z) / Q(z)

% Check roots of Q have positive real parts
solve(Q(z) == 0)

% Check E(y) >= 0
E = Q(1i * y) * Q(-1i * y) - P(1i * y) * P(-1i * y)

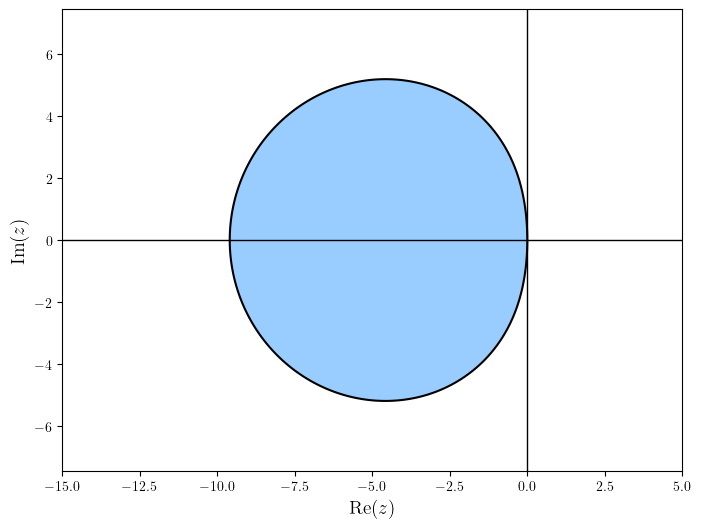
Solution to Exercise 4.3

Determine the stability function

\[\begin{align*} R(z) &= \frac{\left( \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - z \begin{pmatrix} 1/3 & 0 \\ 1 & 0 \end{pmatrix} - z \begin{pmatrix} 3/4 & 0 \\ 0 & 1/4 \end{pmatrix} \right)}{ \det \left( \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - z \begin{pmatrix} 1/3 & 0 \\ 1 & 0 \end{pmatrix} \right)} \\ &= \frac{\det \begin{pmatrix} 1 - 13z/12 & 0 \\ -z & 1 - z/4 \end{pmatrix}}{\det \begin{pmatrix} 1 - z/3 & 0 \\ -z & 1 \end{pmatrix}} = \frac{1 + 2/3 z + \frac{5}{48} z^2}{1 - 1/3 z} \end{align*}\]

Plot

../_images/7223602d4eaab3b1bd749bb13cabe23d2d01accde97c4f4f451c94fc5c19ea71.png

Code

Python

Determine stability function

import sympy as sp

# Define RK method
A = sp.Matrix([[sp.Rational(1,3), 0], [1, 0]])
ebT = sp.Matrix([[sp.Rational(3,4), 0], [0, sp.Rational(1,4)]])
I = sp.eye(2)

# Define numerator and denominator functions
def P(z):
    return (I - z * A + z * ebT).det()

def Q(z):
    return (I - z * A).det()


# Calculate R(z)
z, y = sp.symbols('z, y')
Rz = P(z) / Q(z)
print("R(z) = ")
display(sp.nsimplify(Rz))

Plot region of absolute stability

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['text.usetex'] = True  # allows use of LaTeX in labels

# Generate z values
X, Y = np.meshgrid(np.linspace(-10, 10, 200), np.linspace(-10, 10, 200))
Z = X + Y * 1j

# Define stability function
R = (1 + 2 / 3 * Z + 5 / 48 * Z ** 2) / (1 - 1 / 3 * Z)

# Plot stability region
fig = plt.figure(figsize=(8, 6))
plt.contourf(X, Y, abs(R), levels=[0, 1], colors="#99ccff")
plt.contour(X, Y, abs(R), colors= "k", levels=[0, 1])
plt.axhline(0, color="k", linewidth=1)
plt.axvline(0, color="k", linewidth=1)
plt.axis("equal")
plt.axis([-15, 5, -7, 7])
plt.xlabel("$\mathrm{Re}(z)$", fontsize=14)
plt.ylabel("$\mathrm{Im}(z)$", fontsize=14)
plt.show()

MATLAB

Determine stability function

% Define IRK method
A = [1/3, 0 ; 1, 0];
ebT = [3/4, 0 ; 0, 1/4];
I = eye(2);

% Calculate R(z)
syms z y

P = @(z) det(I - z * A + z * ebT);
Q = @(z) det(I - z * A);

Rz = P(z) / Q(z)

Plot region of absolute stability

% Generate z values
[X, Y] = meshgrid(linspace(-10, 10, 200), linspace(-10, 10, 200));
Z = X + Y * 1i;

% Define stability function
R = (1 + 2 / 3 * Z + 5 / 48 * Z .^ 2) ./ (1 - 1 / 3 * Z);

% Plot stability region
contourf(X, Y, abs(R), [0, 1], LineWidth=2)
xline(0, LineWidth=2)
yline(0, LineWidth=2)
colormap([153, 204, 255 ; 255, 255, 255] / 255)
axis equal
axis([-15, 5, -7, 7])
xlabel("$\mathrm{Re}(z)$", FontSize=12, Interpreter="latex")
ylabel("$\mathrm{Im}(z)$", FontSize=12, Interpreter="latex")

Solution to Exercise 4.4

Calculate the eigenvalues of the coefficient matrix

\[\begin{align*} 0 &= \begin{vmatrix} -80.6 - \lambda & 119.4 \\ 79.6 & -120.4 - \lambda \end{vmatrix} = \lambda^2 + 201 \lambda + 200, \\ \therefore \lambda &= \frac{-201 \pm 199}{2} = -200, -1 \end{align*}\]

so the stiffness ratio is \(S = 200\). The Euler method is stable for \(h\lambda \in [-2, 0]\) so the maximum step length is

\[h = \frac{-2}{\min(-200, -1)} = \frac{-2}{-200} = 0.01.\]