Ordinary Differential Equations exercise solutions#
Solutions to the exercises on ordinary differential equations.
Solution to Exercise 1.1
Rearranging the ODE slightly gives \(y' = 1 - y -e^{-t}\). The values of \(t_n\) are
\[\begin{split} \vec{t} = \begin{pmatrix} 0.0 \\ 0.5 \\ 1.0 \\ 1.5 \\ 2.0 \\ 2.5 \\ 3.0 \\ 3.5 \\ 4.0 \end{pmatrix}, \end{split}\]
and applying the Euler method with step length \(h=0.5\) gives
\[\begin{split} \begin{align*}
y_0 &= 1, \\
y_1 &= y_0 + h (1 - y_0 - e^{-t_0}) \\
&= 1.0 + 0.5 (1 - 1.0 - e^{-0.0}) = 0.5, \\
y_2 &= y_1 + h (1 - y_1 - e^{-t_1}) \\
&= 0.5 + 0.5 (1 - 0.5 - e^{-0.5}) = 0.446735, \\
y_3 &= y_2 + h (1 - y_2 - e^{-t_2}) \\
&= 0.446735 + 0.5 (1 - 0.446735 - e^{-1.0}) = 0.539428, \\
y_4 &= y_3 + h (1 - y_3 - e^{-t_3}) \\
&= 0.539428 + 0.5 (1 - 0.539428 - e^{-1.5}) = 0.658149, \\
y_5 &= y_4 + h (1 - y_4 - e^{-t_4}) \\
&= 0.658149 + 0.5 (1 - 0.658149 - e^{-2.0}) = 0.761407, \\
y_6 &= y_5 + h (1 - y_5 - e^{-t_5}) \\
&= 0.761407 + 0.5 (1 - 0.761407 - e^{-2.5}) = 0.839661, \\
y_7 &= y_6 + h (1 - y_6 - e^{-t_6}) \\
&= 0.839661 + 0.5 (1 - 0.839661 - e^{-3.0}) = 0.894937, \\
y_8 &= y_7 + h (1 - y_7 - e^{-t_7}) \\
&= 0.894937 + 0.5 (1 - 0.894937 - e^{-3.5}) = 0.93237, \\
\end{align*} \end{split}\]
Solution to Exercise 1.2
Table
| t | Euler | Exact | Error |
|:----:|:--------:|:--------:|:--------:|
| 0.00 | 1.000000 | 1.000000 | 0.00e+00 |
| 0.50 | 0.500000 | 0.696735 | 1.97e-01 |
| 1.00 | 0.446735 | 0.632121 | 1.85e-01 |
| 1.50 | 0.539428 | 0.665305 | 1.26e-01 |
| 2.00 | 0.658149 | 0.729329 | 7.12e-02 |
| 2.50 | 0.761407 | 0.794788 | 3.34e-02 |
| 3.00 | 0.839661 | 0.850639 | 1.10e-02 |
| 3.50 | 0.894937 | 0.894309 | 6.28e-04 |
| 4.00 | 0.932370 | 0.926737 | 5.63e-03 |
Plot
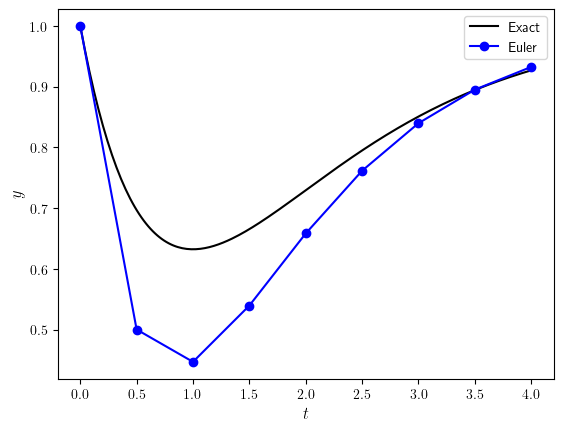
Code
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['text.usetex'] = True # use LaTeX commands in plot
def solveIVP(f, tspan, y0, h, solver):
# Initialise t and y arrays
t = np.arange(tspan[0], tspan[1] + h, h)
y = np.zeros((len(t),len(y0)))
t[0] = tspan[0]
y[0,:] = y0
# Loop through steps and calculate single step solver solution
for n in range(len(t) - 1):
y[n+1,:] = solver(f, t[n], y[n,:], h)
return t, y
def euler(f, t, y, h):
return y + h * f(t, y)
def f(t,y):
return 1 - y - np.exp(-t)
def exact(t):
return 1 - t * np.exp(-t)
# Define IVP parameters
tspan = [0, 4] # boundaries of the t domain
y0 = [1] # initial value
h = 0.5 # step length
# Solve the IVP using the Euler method
t, y = solveIVP(f, tspan, y0, h, euler)
# Print table of solution values
print("| t | Euler | Exact | Error |")
print("|:----:|:--------:|:--------:|:--------:|")
for n in range(len(t)):
print(f"| {t[n]:0.2f} | {y[n,0]:0.6f} | {exact(t[n]):0.6f} | {abs(y[n,0] - exact(t[n])):0.2e} |")
# Calculate exact solution
texact = np.linspace(tspan[0], tspan[1], 200)
yexact = exact(texact)
# Plot solution
fig, ax = plt.subplots()
plt.plot(texact, yexact, 'k-', label='Exact')
plt.plot(t, y[:,0], "b-o", label='Euler')
plt.xlabel("$t$", fontsize=12)
plt.ylabel("$y$", fontsize=12)
plt.legend()
% Define ODE function and exact solution
f = @(t,y) 1 - y - exp(-t);
exact = @(t) 1 - t .* exp(-t);
% Define IVP parameters
tspan = [0, 4];
y0 = 1;
h = 0.5;
% Solve the IVP using the Euler method
[t, y] = solveIVP(f, tspan, y0, h, @euler);
% Print table of solution values
for i = 1:1
fprintf("| t | Euler | Exact | Error |")
fprintf("|:----:|:---------:|:---------:|:--------:|")
for n = 1 : length(t)
fprintf("| %1.2f | %9.6f | %9.6f | %1.2e |\n", t(n), y(n), exact(t(n)), abs(y(n) - exact(t(n))));
end
end
% Calculate exact solution (for plotting)
texact = linspace(tspan(1), tspan(2), 200);
yexact = exact(texact);
% Plot solution
plot(texact, yexact, 'k-', LineWidth=1)
hold on
plot(t, y, 'b-o', LineWidth=1, MarkerFaceColor='b')
hold off
axis padded
xlabel('$t$', FontSize=14, Interpreter='latex')
ylabel('$y$', FontSize=14, Interpreter='latex')
legend('Exact', 'Euler', fontsize=12)
% --------------------------------------------------------
function [t, y] = solveIVP(f, tspan, y0, h, solver)
% Define t and y arrays
t = (tspan(1) : h : tspan(2));
y = zeros(length(t), length(y0));
y(1,:) = y0;
% Loop through the steps and calculate single step solver solution
for n = 1 : length(t) - 1
y(n+1,:) = solver(f, t(n), y(n,:), h);
end
end
% --------------------------------------------------------
function y = euler(f, t, y, h)
y = y + h * f(t, y);
end
Solution to Exercise 1.3
(a)
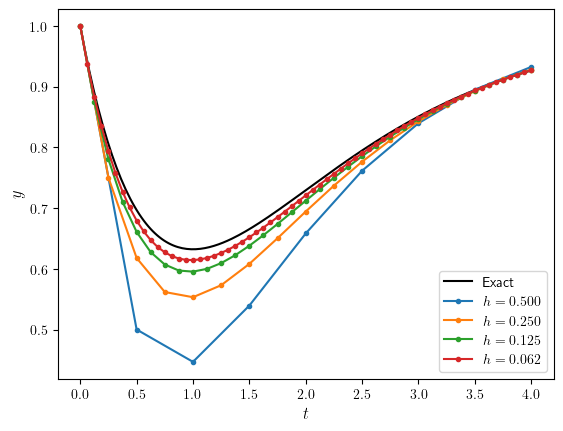
# Plot the exact solution
fig, ax = plt.subplots()
plt.plot(texact, yexact, 'k-', label='Exact')
# Loop through h values and calculate the solutions
hvals = [0.5, 0.25, 0.125, 0.0625]
for h in hvals:
t, y = solveIVP(f, tspan, y0, h, euler)
plt.plot(t, y, '.-', label=f"$h = {h:0.3f}$")
plt.xlabel("$t$", fontsize=12)
plt.ylabel("$y$", fontsize=12)
plt.legend()
plt.show()
% Plot the exact solution
plot(texact, yexact, 'k', LineWidth=1)
hold on
% Loop through h values and calculate the solutions
hvals = [0.5, 0.25, 0.125, 0.0625];
for h = hvals
[t, y] = solveIVP(f, tspan, y0, h, @euler);
plot(t, y, 'o-')
end
xlabel('$t$', FontSize=14, Interpreter='latex')
ylabel('$y$', FontSize=14, Interpreter='latex')
legend('Exact', '$h=0.5$', '$h=0.25$', '$h=0.125$', '$h=0.0625$', ...
Location='southeast', FontSize=12, Interpreter='latex')
hold off
(b) Exact solution: \(y(1) = 1 - e^{-1} = 0.632121\)
Table
| h | Euler | Error |
|:-----:|:---------:|:--------:|
| 0.500 | 0.446735 | 1.85e-01 |
| 0.250 | 0.553196 | 7.89e-02 |
| 0.125 | 0.595324 | 3.68e-02 |
| 0.062 | 0.614319 | 1.78e-02 |
Plot
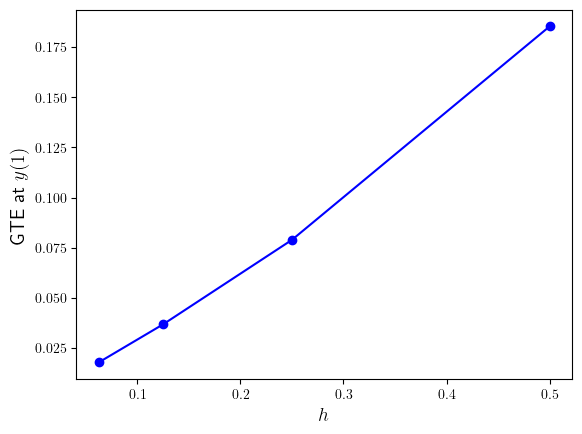
errors = []
print(f"Exact solution: y(1) = {exact(1):0.6f}\n")
print("| h | Euler | Error |")
print("|:-----:|:---------:|:--------:|")
for h in hvals:
t, y = ivp_solver(f, tspan, y0, h, euler)
idx = np.argmin(abs(t - 1))
errors.append(abs(y[idx,0] - exact(1)))
print(f"| {h:0.3f} | {y[idx,0]:9.6f} | {errors[-1]:0.2e} |")
# Plot errors
fig, ax = plt.subplots()
plt.plot(hvals, errors, 'b-o')
plt.xlabel('$h$', fontsize=14)
plt.ylabel('GTE at $y(1)$', fontsize=14)
plt.show()
for i = 1 : 1
errors = [];
fprintf("Exact solution: y(1) = %1.6f\n", exact(1))
fprintf("| h | Euler | Error |")
fprintf("|:-----:|:--------:|:--------:|")
for h = hvals
[t, y] = solveIVP(f, tspan, y0, h, @euler);
[~, idx] = min(abs(t - 1));
errors = [errors, abs(y(idx,1) - exact(1))];
fprintf("| %1.2f | %9.6f | %1.2e |\n", h, y(idx), errors(end))
end
end
% Plot errors
plot(hvals, errors, 'b-o', LineWidth=2, MarkerFaceColor='b')
axis padded
xlabel('$h$', FontSize=14, Interpreter='latex')
ylabel('GTE at $y(1)$', FontSize=14, Interpreter='latex')
(c) The plot of the global truncation error for \(y(1)\) shows that the errors tend to zero as \(h\) decreases in a roughly linear fashion indicating that the Euler method is first-order accurate.
Solution to Exercise 1.4
Let \(y_1 = \theta\) and \(y_2 = \dot{\theta}\) then we can write the ODE as
\[\begin{split} \begin{align*}
y_1' &= y_2, \\
y_2' &= -\frac{g}{L} \sin(y_1),
\end{align*} \end{split}\]
so we have the IVP \(\vec{y}' = \vec{f}(t, \vec{y})\) where
\[\begin{split} \begin{align*}
\vec{y} &= \begin{pmatrix} y_1 \\ y_2 \end{pmatrix}, &
\vec{f}(t, \vec{y}) &= \begin{pmatrix} y_2 \\ -g \sin(y_1)/L \end{pmatrix}, &
\vec{y}_0 &= \begin{pmatrix} \pi/2 \\ 0 \end{pmatrix}.
\end{align*} \end{split}\]
Plot
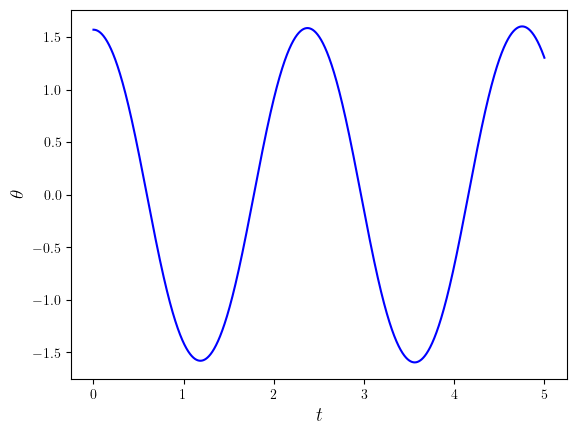
Code
# Define ODE function
def f(t, y):
return np.array([y[1], -g / L * np.sin(y[0])])
# Define IVP
tspan = [0, 5]
y0 = [np.pi / 2, 0]
h = 0.001
g = 9.81 # acceleration due to gravity
L = 1 # pendulum length
# Calculate the solution to the IVP
t, y = solveIVP(f, tspan, y0, h, euler)
# Plot solution
fig, ax = plt.subplots()
plt.plot(t, y[:,0], "b-")
plt.xlabel("$t$", fontsize=14)
plt.ylabel("$\\theta$", fontsize=14)
% Define ODE
f = @(t, y) [y(2), -9.81 * sin(y(1))];
% Define IVP
tspan = [0, 5];
y0 = [pi / 2, 0];
h = 0.001;
g = 9.81;
L = 1;
% Solve IVP
[t, y] = solveIVP(f, tspan, y0, h, @euler);
% Plot solution
plot(t, y(:, 1), "b-", LineWidth=2, MarkerFaceColor="b")
xlabel("$t$", FontSize=16, Interpreter="latex")
ylabel("$\theta$", FontSize=16, Interpreter="latex")