1.1. The Euler method

Fig. 1.2 Leonard Euler (1707 - 1783)

The Euler method named after Swiss mathematician Leonard Euler (pronounced “Oy-ler”) is the simplest numerical method used to solve ODEs. Consider the general first-order IVP

\[ y' = f(t, y), \qquad y(t_0) = y_0, \]

where the solution is \(y(t)\). The tangent line for \(y(t)\) where \(t = t_0\) has the gradient \(f(t_0, y_0)\) is shown in Fig. 1.3.

Fig. 1.3 The derivation of the Euler method.

The equation of this tangent line is

\[ y = y_0 + f(t_0, y_0) (t - t_0). \]

We can approximate the value of \(y(t_1)\) where \(t_1\) is close to \(t_0\) by calculating the point on the tangent where \(t = t_1\)

\[ y_1 = y_0 + f(t_0, y_0) (t_1 - t_0). \]

Assuming that \(y_1\) is a reasonable approximation of \(y(t_1)\) then we can approximate the value of \(y(t_2)\) using the the tanget line at \(t = t_1\). The gradient of this tangent line is \(f(t_1, y_1)\) so

\[ y_2 = y_1 + f(t_1, y_1) (t_2 - t_1). \]

Doing similar for more points along the \(t\) domain

\[\begin{split} \begin{align*} y_3 &= y_2 + f(t_2, y_2) (t_3 - t_2), \\ y_4 &= y_3 + f(t_3, y_3) (t_4 - t_3), \\ & \vdots \\ y_{n+1} &= y_n + f(t_n, y_n) (t_{n+1} - t_n). \end{align*} \end{split}\]

If we use equally spaced points for \(t_0, t_1, t_2, \ldots\) such that \(t_{n+1} - t_n = h\) then the approximation of the solution at \(t_{n+1}\) is

\[ y_{n+1} = y_n + h f(t_n, y_n), \]

which is the Euler method.

Definition 1.3 (The Euler method)

The Euler method for solving the initial value problem \(y' = f(t, y)\), \(t \in [t_0, t_{\max}]\), \(y(t_0) = y_0\) is

(1.2)\[y_{n+1} = y_n + h f(t_n ,y_n),\]

where \(h = t_{n+1} - t_n\).

1.1.1. Solving an IVP using the Euler method

To solve an IVP using the Euler method we choose a value of the step length \(h\) and calculate the number of steps required to step through the domain \(t \in [t_0, t_{\max}]\). Using a constant step length \(h\) then \(t_n\) is

\[ t_n = t_0 + nh,\]

so

\[ nsteps = \operatorname{int} \left( \frac{t_{\max} - t_0}{h} \right). \]

We then calculate \(y_1\) using equation (1.2) and \(t_1 = t_0 + h\). Then we use the values of \(t_1\) and \(y_1\) to calculate the values of \(y_2\) and \(t_2\) and continue this way until we have calculated \(y_n\) and \(t_n\) across the domain \([t_0, t_{\max}]\). The Euler method is an example of a single step method since it only requires information from a single step of the solution to calculate the next step. The other type of numerical method for solving ODEs is the linear multistep methods that requires information from multiple previous steps.

Algorithm 1.1 (Solving an IVP using the Euler method)

Inputs A first-order ODE of the form \(y' = f(t,y)\), a domain \(t \in [t_0, t_{\max}]\), an initial value \(y(t_0) = y_0\) and a step length \(h\)

Outputs \((t_0, t_1, \ldots)\) and \((y_0, y_1, \ldots)\)

• \(nsteps \gets \operatorname{int}\left( \dfrac{t_{\max} - t_0}{h} \right)\)

• For \(n = 0, \ldots, nsteps\)

  • \(y_{n+1} \gets y_n + hf(t_n, y_n)\)

  • \(t_{n+1} \gets t_n + h\)

• Return \((t_0, t_1, \ldots)\) and \((y_0, y_1, \ldots)\)

Example 1.1

Calculate the solution to the following initial value problem using the Euler method with \(h = 0.2\)

\[y' = ty, \qquad t\in [0,1], \qquad y(0)=1.\]

Solution (click to show)

Here the ODE function is \(f(t, y) = ty\), \(t_0 = 0\), \(y_0 = 1\) and \(h = 0.2\). First, we calculate the number of steps required

\[ nsteps = \operatorname{int} \left( \frac{t_{\max} - t_0}{h} \right) = \operatorname{int} \left( \frac{1 - 0}{0.2} \right) = 5. \]

We then step through the Euler method

\[\begin{split} \begin{align*} y_1 &= y_0 + h (t_0 y_0) = 1 + 0.2(0)(1) = 1, \\ t_1 &= t_0 + h = 0 + 0.2 = 0.2, \\ \\ y_2 &= y_1 + h (t_1 y_1) = 1 + 0.2(0.2)(1) = 1.04, \\ t_2 &= t_1 + h = 0.2 + 0.2 = 0.4, \\ \\ y_3 &= y_2 + h (t_2 y_2) = 1.04 + 0.2(0.4)(1.04) = 1.1232, \\ t_3 &= t_2 + h = 0.4 + 0.2 = 0.6, \\ \\ y_4 &= y_3 + h (t_3 y_3) = 1.1232 + 0.2(0.6)(1.1232) = 1.257984, \\ t_4 &= t_3 + h = 0.6 + 0.2 = 0.8, \\ \\ y_5 &= y_4 + h (t_4 y_4) = 1.257984 + 0.2(0.8)(1.257984) = 1.459261, \\ t_5 &= t_4 + h = 0.8 + 0.2 = 1.0. \end{align*} \end{split}\]

So the solution to this IVP using the Euler method is

\(t_n\)	\(y_n\)
0.00	1.000000
0.20	1.000000
0.40	1.040000
0.60	1.123200
0.80	1.257984
1.00	1.459261

1.1.2. Programming the Euler method

You may have noticed that calculating the solution to an initial value problem using a numerical method using a pen, paper and calculator is a tedious exercise requiring lots of repeated calculations. Fortunately we have computers to do this work for us.

Below is a function called euler() which solves an IVP using the Euler method.

Python

def euler(f, tspan, y0, h):

    nsteps = int((tspan[1] - tspan[0]) / h)
    t = np.zeros(nsteps + 1)
    y = np.zeros(nsteps + 1)
    t[0] = tspan[0]
    y[0] = y0

    for n in range(nsteps):
        y[n+1] = y[n] + h * f(t[n], y[n])
        t[n+1] = t[n] + h

    return t, y

MATLAB

function [t, y] = euler(f, tspan, y0, h)

nsteps = floor((tspan(2) - tspan(1)) / h);
t = zeros(nsteps + 1, 1);
y = zeros(length(t), 1);
y(1) = y0;

for n = 1 : length(t) - 1
    y(n+1) = y(n) + h * f(t(n), y(n));
    t(n+1) = t(n) + h;
end

end

The inputs to the function are:

• f - the name of the ODE function to be solved (this needs to be defined elsewhere)

• tspan - an array containing the two values \(t_0\) and \(t_{\max}\)

• y0 - the initial value of the solution to the ODE \(y(t_0)\)

• h - the step length

The function first calculates creates two arrays t and y which store the values of \(t\) and \(y\) and the first element of y is set equal to y0. A for loop is used to step through the domain and calculate the solution at each step using the Euler method.

The code below solves the IVP from Example 1.1, solves it using the Euler method and outputs a table containing the solution values and a plot of \(y\) against \(t\).

Python

import numpy as np
import matplotlib.pyplot as plt

# Define Euler method function
def euler(f, tspan, y0, h):

    nsteps = int((tspan[1] - tspan[0]) / h)
    t = np.zeros(nsteps + 1)
    y = np.zeros(nsteps + 1)
    t[0] = tspan[0]
    y[0] = y0
    
    for n in range(nsteps):
        y[n+1] = y[n] + h * f(t[n], y[n])
        t[n+1] = t[n] + h

    return t, y


# Define the ODE function
def f(t, y):
    return t * y


# Define IVP parameters
tspan = [0, 1]  # boundaries of the t domain
y0 = 1          # initial value of the solution
h = 0.2         # step length

# Solve using the Euler method
t, y = euler(f, tspan, y0, h)

# Print table of solution values
print("|  t   |     y     | ")
print("|:----:|:---------:|")
for n in range(len(t)):
    print(f"| {t[n]:4.2f} | {y[n]:9.6f} |")

# Plot solution
fig, ax = plt.subplots()
plt.plot(t, y, "bo-", label="Euler")
plt.xlabel("$t$", fontsize=12)
plt.ylabel("$y(t)$", fontsize=12)
plt.show()

MATLAB

% Define ODE function
f = @(t, y) t * y;

% Define IVP parameters
tspan = [0, 1]; % boundaries of the t domain
y0 = 1;         % initial value of the solution
h = 0.2;        % step length

% Solve IVP using the Euler method
[t, y] = euler(f, tspan, y0, h);

% Print table of solution values (for loop is used to group print statements)
for i = 1 : 1
    fprintf("|  t   |     y     |\n|:----:|:---------:|");
    for n = 1 : length(t)
        fprintf("\n| %4.2f | %9.6f | %9.6f | %8.2e |", t(n), y(n));
    end
end
% Plot solution
plot(t, y, "b-o", LineWidth=2, MarkerFaceColor="b")
axis padded
xlabel("$t$", FontSize=14, Interpreter="latex")
ylabel("$y(t)$", FontSize=14, Interpreter="latex")

% ----------------------------------------------------
function [t, y] = euler(f, tspan, y0, h)

nsteps = floor((tspan(2) - tspan(1)) / h);
t = zeros(nsteps + 1, 1);
y = zeros(length(t), 1);
y(1) = y0;

for n = 1 : length(t) - 1
    y(n+1) = y(n) + h * f(t(n), y(n));
    t(n+1) = t(n) + h;
end

end

Important

All functions defined in MATLAB must come at the end of the script file beneath all other commands.

The output for this code is shown below.

|  t   |     y     | 
|:----:|:---------:|
| 0.00 |  1.000000 |
| 0.20 |  1.000000 |
| 0.40 |  1.040000 |
| 0.60 |  1.123200 |
| 0.80 |  1.257984 |
| 1.00 |  1.459261 |

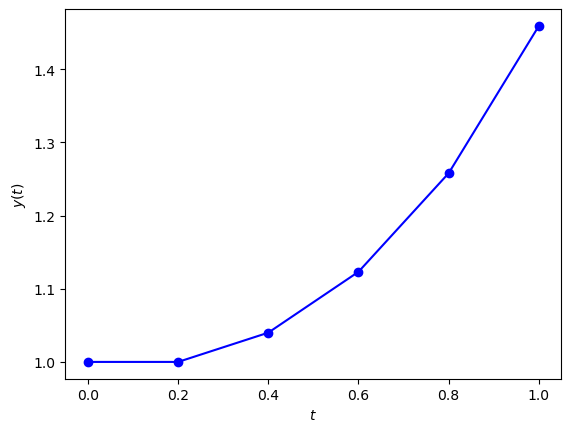
Fig. 1.4 Plot of the IVP \(y' = ty\), \(t\in [0, 1]\), \(y(0) = 1\) using the Euler method with step length \(h=0.2\).