6.6. Contour plots

Contour plots show points of equal value can be produced using the plt.contour() function.

plt.contour(X, Y, Z)

where X, Y and Z are 2D co-ordinate arrays. Lets create a contour plot of the bi-variate function \(f(x, y) = \sin(\pi x)\sin(\pi y)\) that we used in the previous section on surface plots. Enter the following code into your program.

# Contour plot
fig, ax = plt.subplots()
plt.contour(X, Y, Z)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()

Run your program and you should see the following plot added to the Plots pane.

---

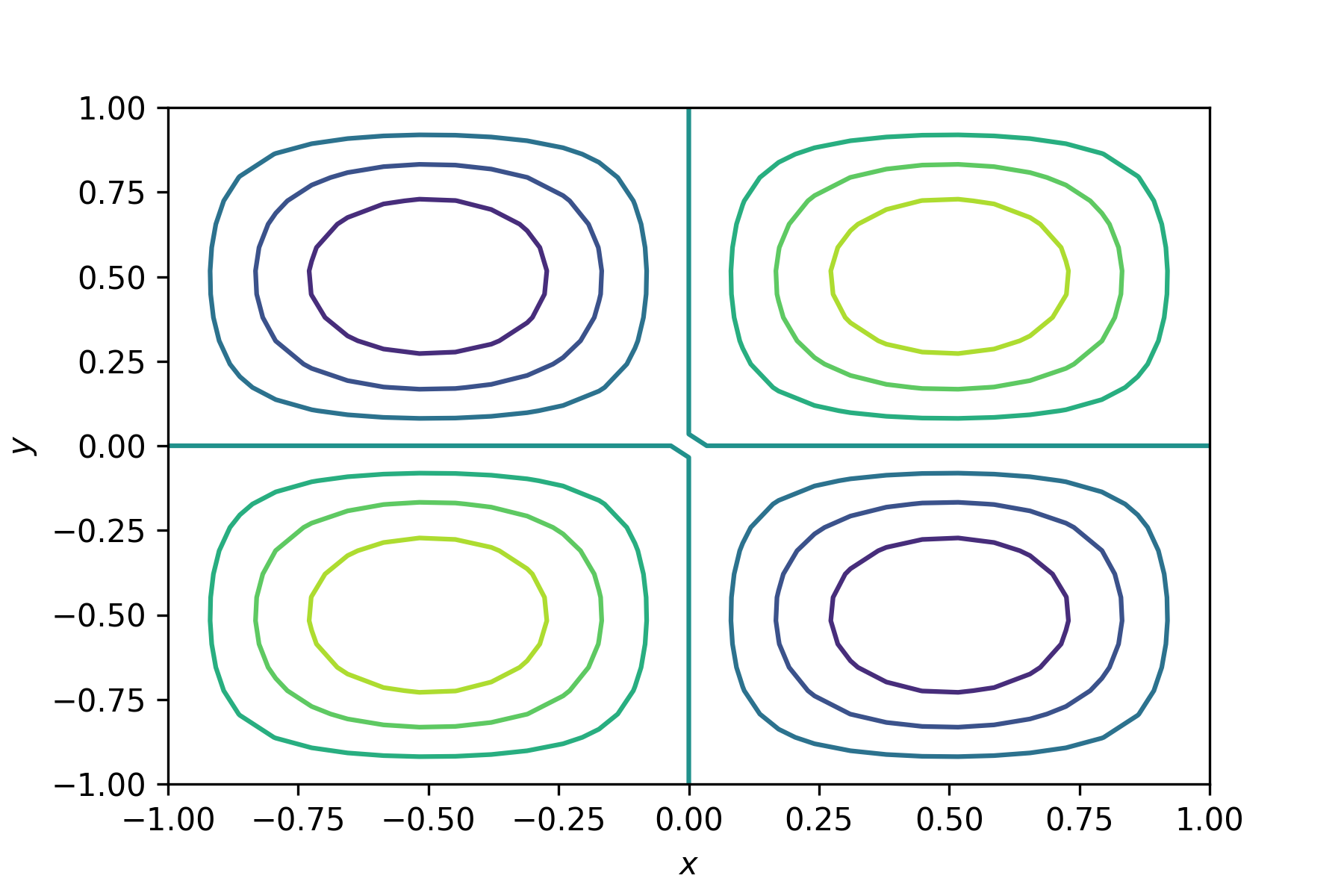
6.6.1. Contour levels

The number of contour lines that are used a draw a contour plot can be specified in the plt.contour() function.

plt.contour(X, Y, Z, levels)

where levels is an integer. To demonstrate this enter the following code into your program before the plt.show() function.

plt.contour(X, Y, Z, 15)

Here we specify that we want 15 contour lines on our contour plot. Run your program and you should see the following added to the Plots pane.

---

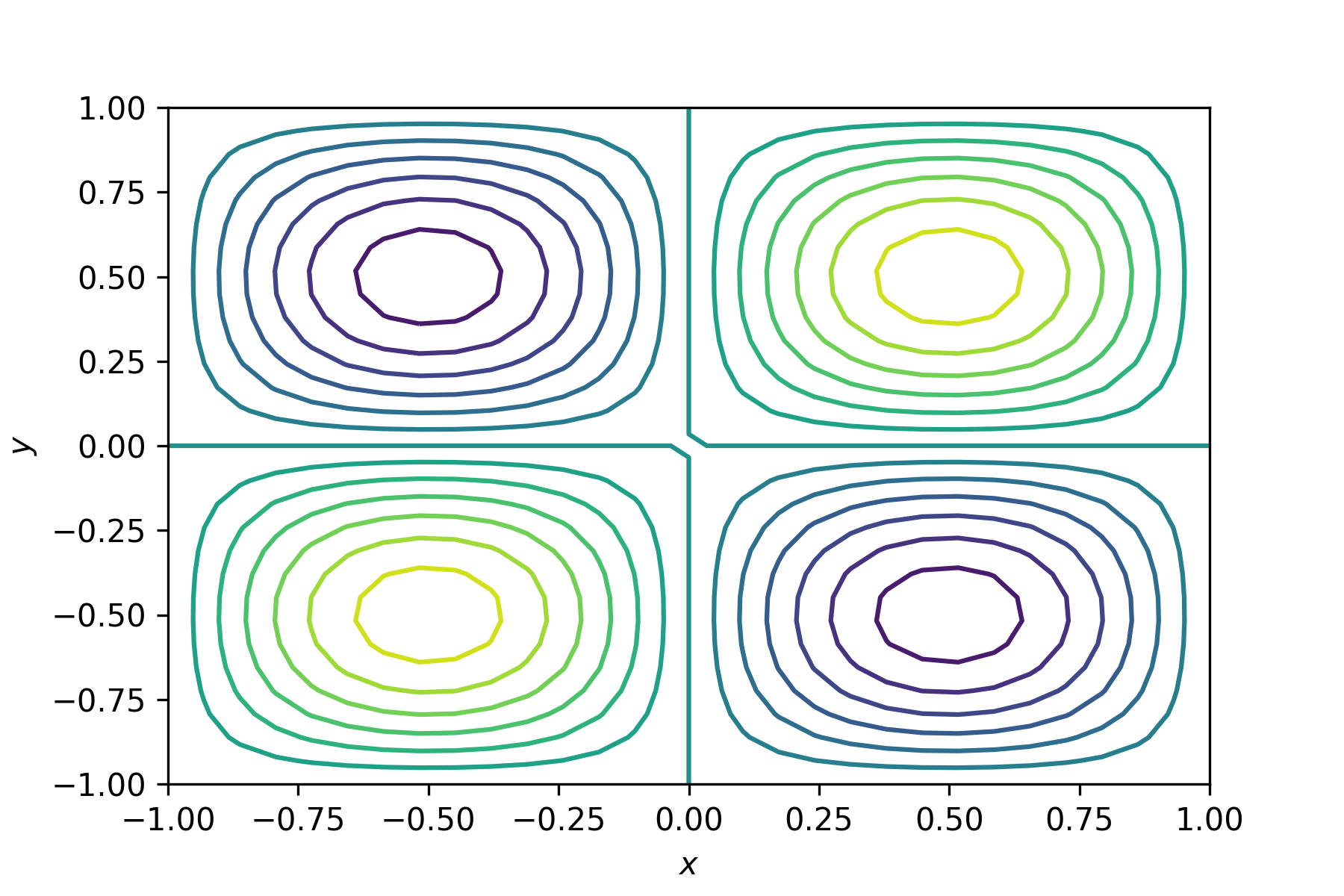
6.6.2. Contour labels

Looking at our contour plots it may be difficult to see which contour lines represent the higher values. To help with this we can add labels to each of our contour lines using the ax.clabel() function.

ax.clabel(plot)

where plot is the name of a plot object. We can assign a name to a plot object like we would any other variable. To demonstrate this enter the following code into your program.

# Contour labels
fig, ax = plt.subplots()
my_contour = plt.contour(X, Y, Z, 12)
ax.clabel(my_contour)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.show()

Here we have created a contour plot and given it the nsame my_contour then added labels to the contour lines. Run your program and you should see the following plot added to the Plots pane.

---

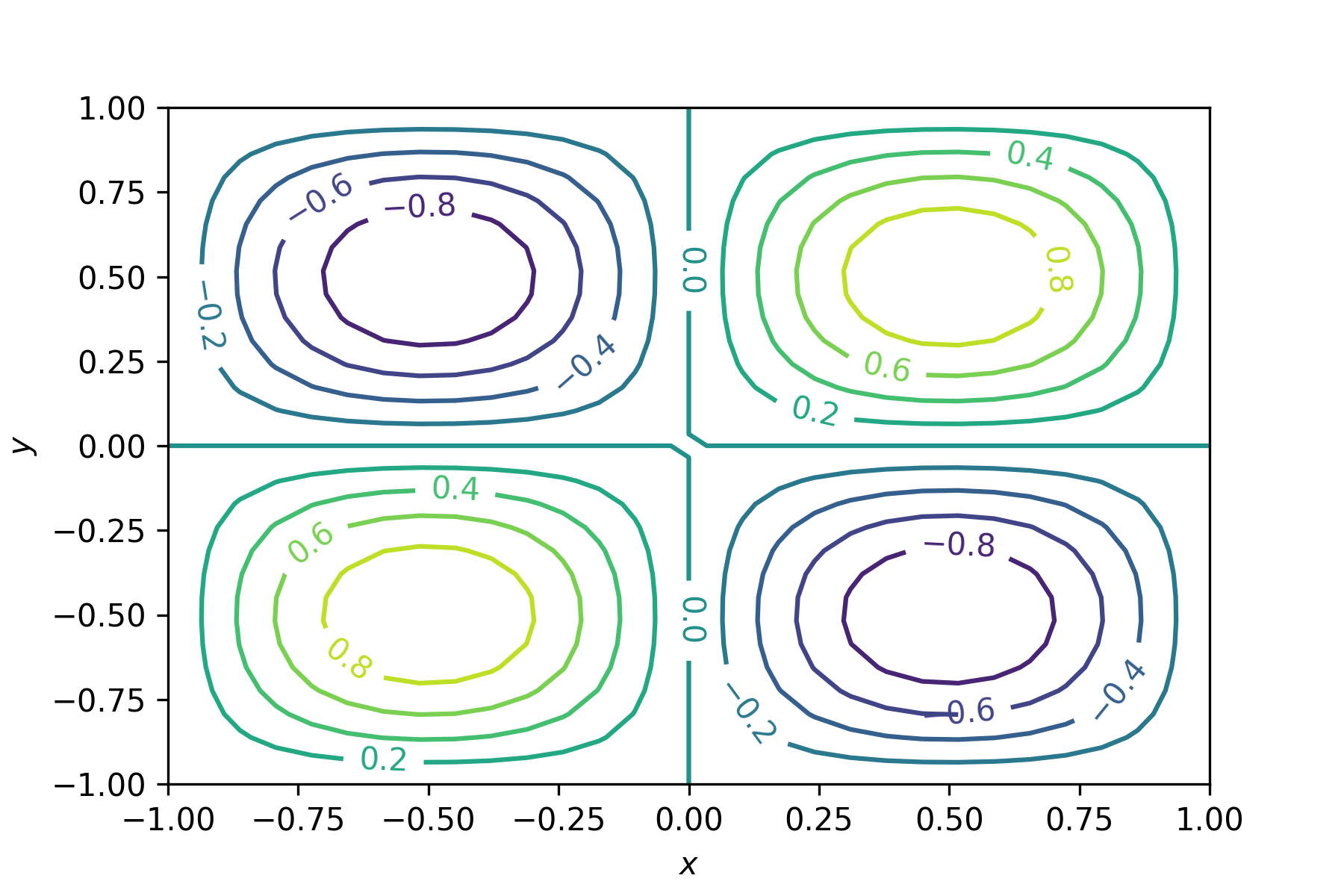
6.6.3. Exercise

Exercise 6.8

Produce a contour plot of the function \(z=(z_1-z_2)^2\) where \(z_1=\exp(-x^2-y^2)\) and \(z_2=\exp(-(x-1)^2-(y-1)^2)\) over the domain \(x,y\in[-2,3]\).