13.4. Surface plots#
Surface plots can then be generated using the surf() function
surf(X, Y, Z)
where X, Y and Z are 2D co-ordinate arrays. To produce a surface plot of the bi-variate function \(z=f(x,y)\) we require \(x\) and \(y\) co-ordinates in the domain. The meshgrid() function is useful for generating these.
X, Y = meshgrid(x, y)
This generates two 2D arrays X and Y from two 1D arrays x and y. X contains the elements of x arranged in rows and Y contains the elements of y arranged in columns. To demonstrate this enter the following code into your program.
% Meshgrid
x = linspace(0, 4, 5);
y = linspace(0, 3, 4);
[X, Y] = meshgrid(x, y);
x
y
X
Y
Run your program and you should see the following added to the command window.
x =
0 1 2 3 4
y =
0 1 2 3
X =
0 1 2 3 4
0 1 2 3 4
0 1 2 3 4
0 1 2 3 4
Y =
0 0 0 0 0
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
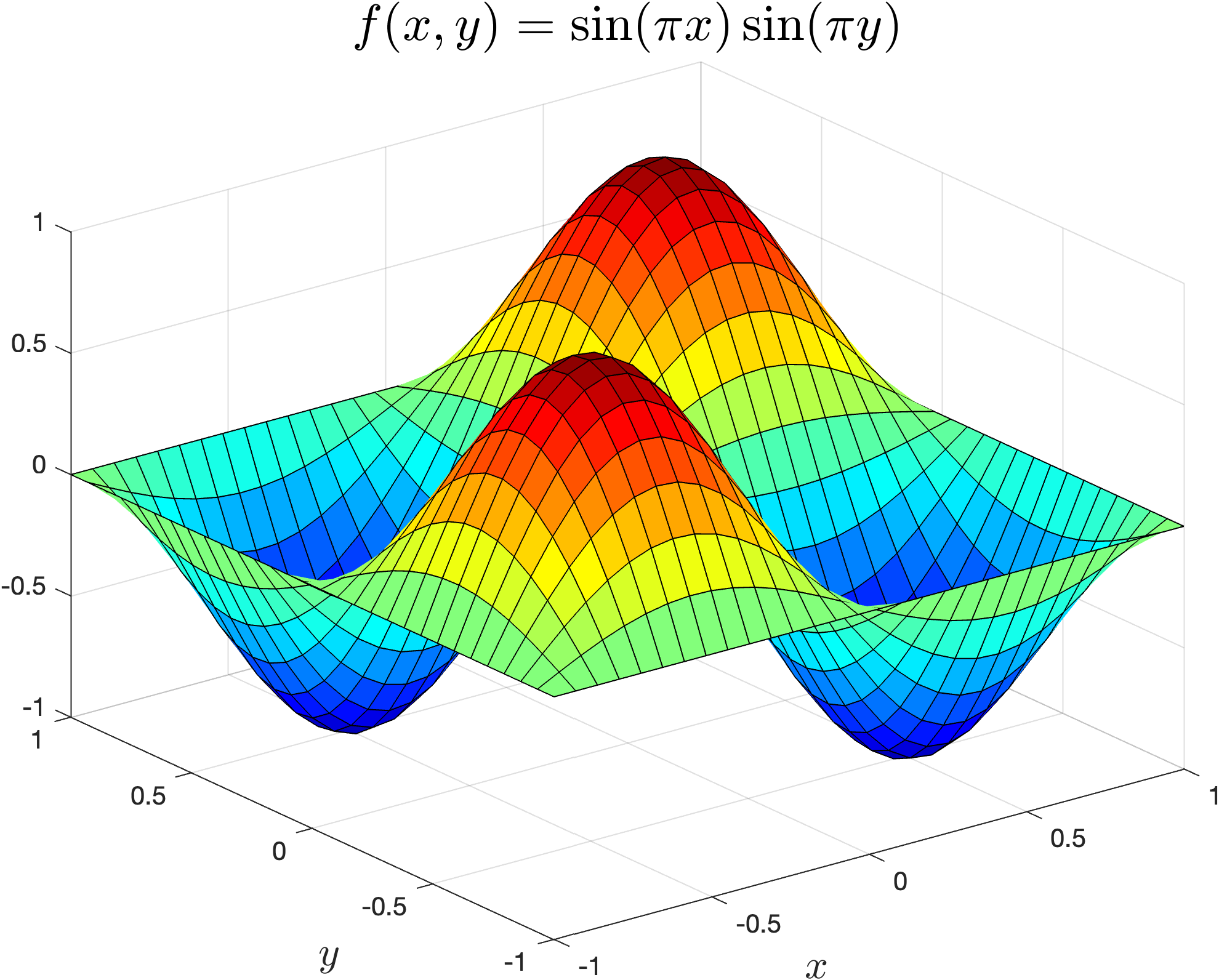
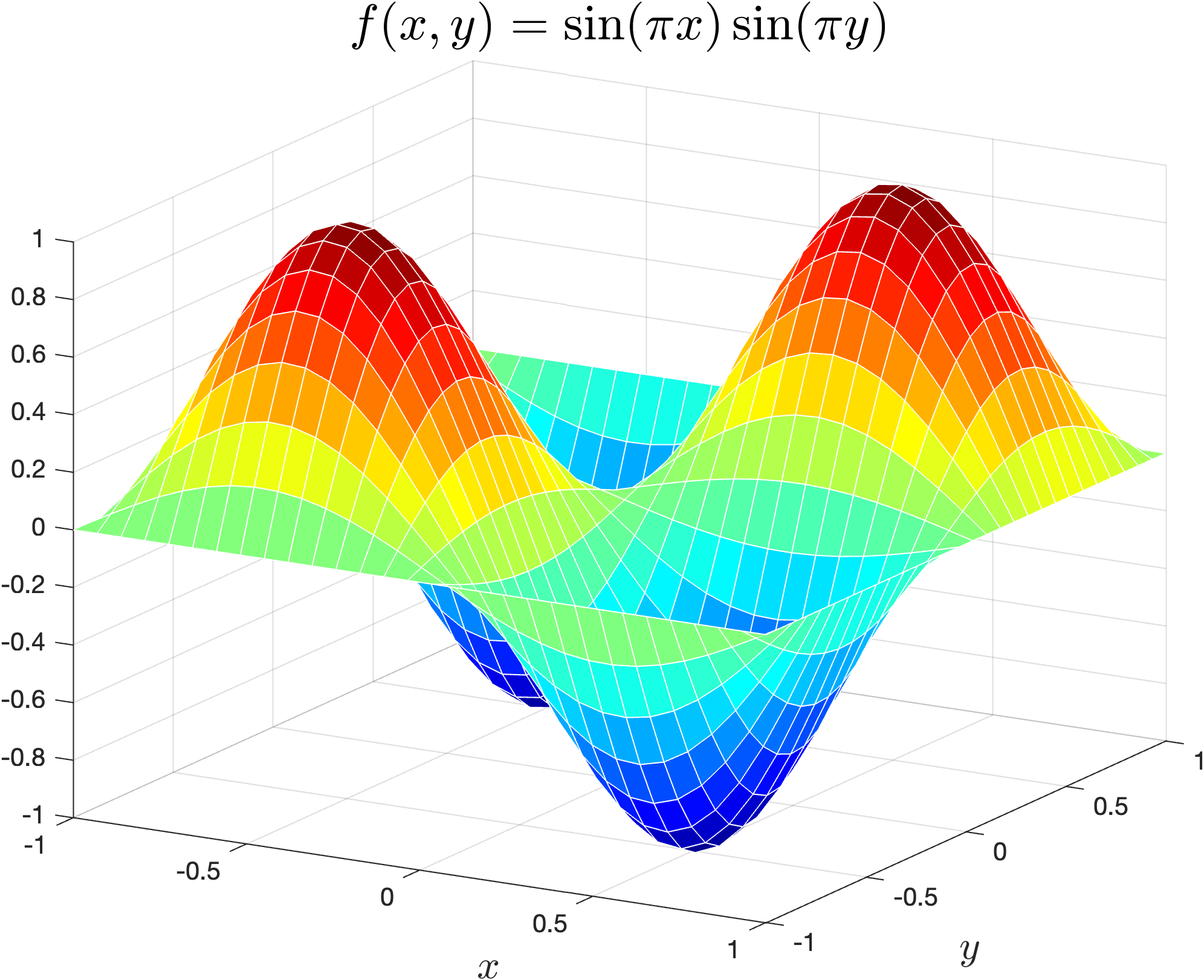
Lets produce a surface plot of the bi-variate function \(f(x, y) = \sin(\pi x) + \cos(\pi y)\) for \(x, y \in [-1, 1]\). Enter the following code into your program.
% Surface plots
x = linspace(-1, 1, 30);
y = linspace(-1, 1, 30);
[X, Y] = meshgrid(x, y);
Z = sin(pi * X) .* sin(pi * Y);
clf
surf(X, Y, Z)
xlabel('$x$', FontSize=16, Interpreter='latex')
ylabel('$y$', FontSize=16, Interpreter='latex')
title('$f(x,y) = \sin(\pi x)\sin(\pi y)$', FontSize=20, Interpreter='latex')
Run your program and you should see the following plot added to the plot window.
13.4.1. Colormaps#
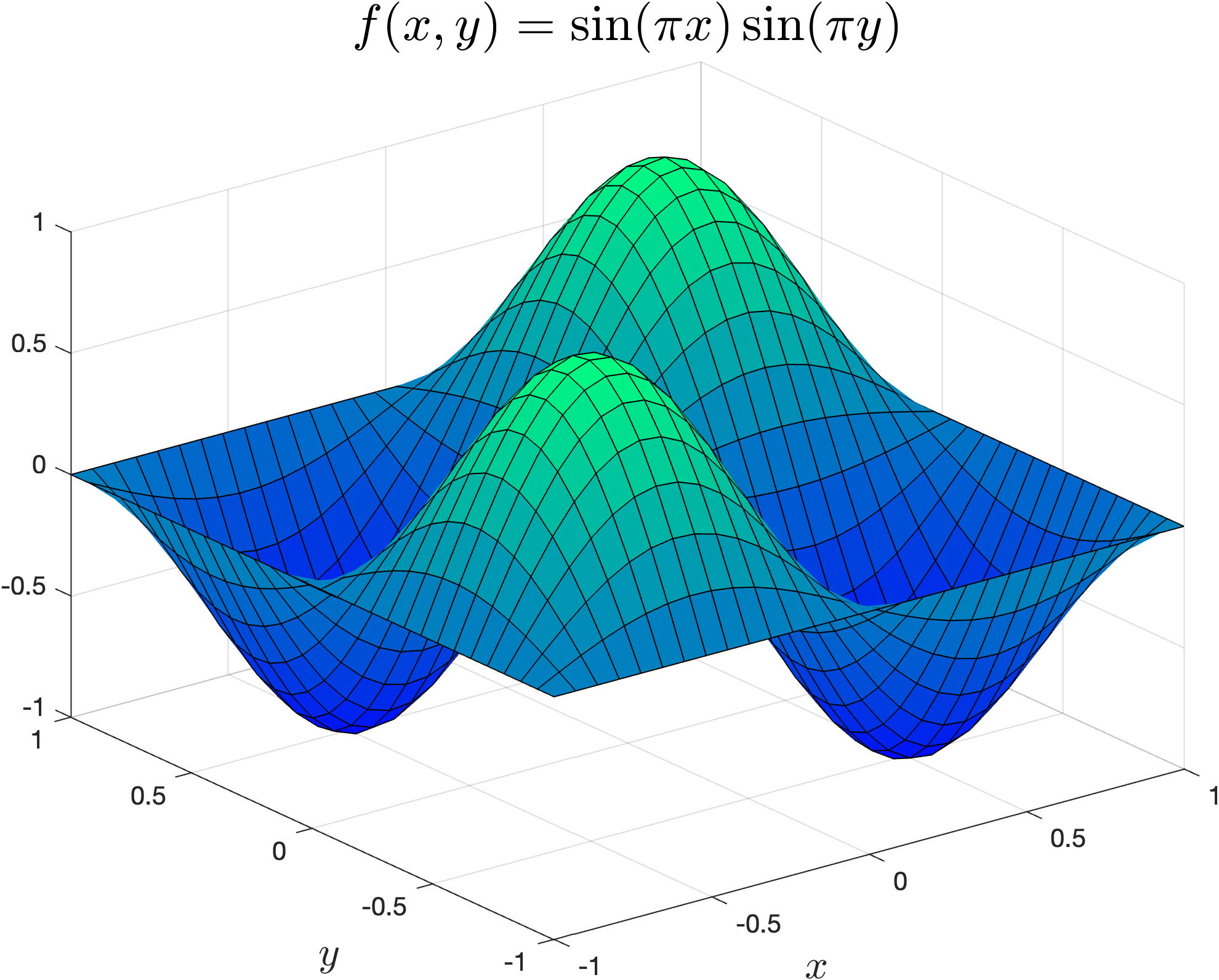
We can add colours to a surface plot in the form of a colormap where the color used for the surface is based on some value, e.g., the height. A colormap can be added to a surface plot using the colormap() function. The surface plot above uses the default MATLAB colormap which is jet.
colormap(name_of_colormap)
where name_of_colormap is the name of the colormap to be applied (see MATLAB Help Center for a list of these). Lets demonstrate this by applying the winter colormap to our surface plot, enter the following code into your program.
colormap(winter)
Run your program and you should see the following plot added to the plot window.
13.4.2. Line colour#
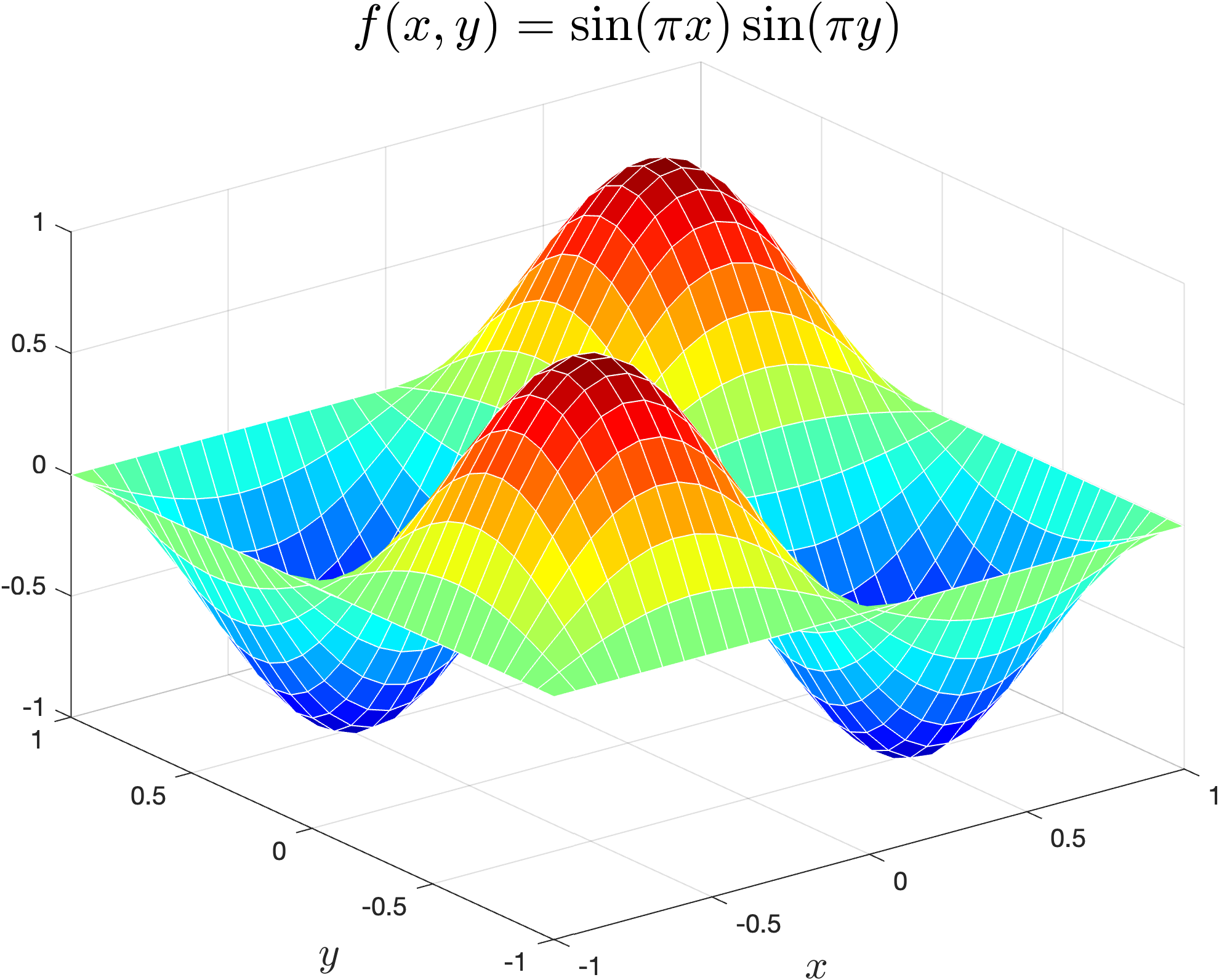
The default line colour for MATLAB surface plots is black which is fine for the majority of plots. However, the line colour can be changed if needed using the EdgeColor property
surf(X, Y, Z, EdgeColor='colour')
Lets change the line colour of our surface plot to white, change your code so that the plotting command looks like the following.
surf(X, Y, Z, EdgeColor='w')
Run your program and you should see the following plot added to the plot window.
13.4.3. View angle#
With 3D plots we can control the position of the viewpoint using the view_init() function
view(elevation, azimuth)
where elevation and azimuth are the angles (in degrees) that specify the vertical and horizontal position of the viewpoint relative to the centre of view (Fig. 13.7).
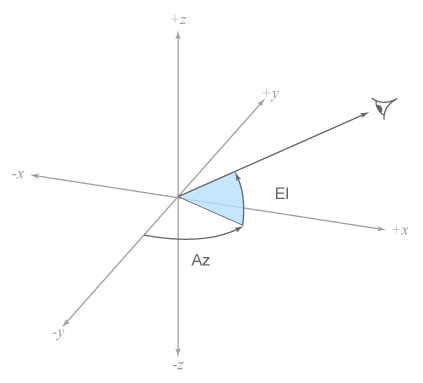
Fig. 13.7 Azimuth and elevation angles (from MATLAB Help Center)#
Lets view our surface plot from an azimuth angle of 30\(^\circ\) and an elevation of 20\(^\circ\). Enter the following code into your program.
% View angle
view_init(20, 30)
Run your program and you should see the following plot added to the plot window.
13.4.4. Exercise#
Exercise 13.7
Produce a surface plot of the function \(f(x, y) = \exp(-20((x - 0.5)^2 + (y - 0.5)^2))\) over the domain \(x,y \in [0, 1]\) using the autumn colormap.