Linear Transformations

Solution to Exercise 6.1

(a) Let \(\vec{u} = (u_1, u_2)^\mathsf{T}, \vec{v} = (v_1, v_2)^\mathsf{T} \in \mathbb{R}^2\) and \(\alpha \in \mathbb{R}\)

\[\begin{split} \begin{align*} T(\vec{u} + \alpha \vec{v}) &= T\begin{pmatrix} u_1 + \alpha v_1 \\ u_2 + \alpha v_2 \end{pmatrix} = \begin{pmatrix} 0 \\ u_2 + \alpha v_2 \end{pmatrix}, \\ T(\vec{u}) + \alpha T(\vec{v}) &= T\begin{pmatrix} u_1 \\ u_2 \end{pmatrix} + \alpha T \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = \begin{pmatrix} 0 \\ u_2 + \alpha v_2 \end{pmatrix}, \end{align*} \end{split}\]

therefore \(T\) is a linear transformation.

(b) \(T\) is not a linear transformation since

\[\begin{split} \begin{align*} T\left( \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \end{pmatrix} \right) = \begin{pmatrix} 2 \\ 5 \end{pmatrix}, \\ T\begin{pmatrix} 1 \\ 0 \end{pmatrix} + T\begin{pmatrix} 1 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 \\ 10 \end{pmatrix}. \end{align*} \end{split}\]

(c) Let \(\vec{u} = (u_1, u_2)^\mathsf{T}, \vec{v} = (v_1, v_2)^\mathsf{T} \in \mathbb{R}^2\) and \(\alpha \in \mathbb{R}\)

\[\begin{split} \begin{align*} T(\vec{u} + \alpha \vec{v}) &= T\begin{pmatrix} u_1 + \alpha v_1 \\ u_2 + \alpha v_2 \end{pmatrix} = \begin{pmatrix} u_1 + \alpha v_1 \\ u_1 - u_2 + \alpha v_1 - \alpha v_2 \end{pmatrix}, \\ T(\vec{u}) + \alpha T(\vec{v}) &= T\begin{pmatrix} u_1 \\ u_2 \end{pmatrix} + \alpha T\begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = \begin{pmatrix} u_1 + \alpha v_1 \\ u_1 + \alpha v_1 - u_2 - \alpha v_2\end{pmatrix}, \end{align*} \end{split}\]

therefore \(T\) is a linear transformation.

(d) Let \(\vec{u} = (u_1, u_2, v_3)^\mathsf{T},\vec{v} = (v_1, v_2, v_3)^\mathsf{T}\in \mathbb{R}^3\) and \(\alpha \in \mathbb{R}\)

\[\begin{split} \begin{align*} T(\vec{u} + \alpha \vec{v}) &= T\begin{pmatrix} u_1 + \alpha v_1 \\ u_2 + \alpha v_2 \\ u_3 + \alpha v_3 \end{pmatrix} = \begin{pmatrix} u_1 + u_2 + \alpha v_1 + \alpha v_2 \\ u_3 + \alpha v_3 \end{pmatrix} , \\ T(\vec{u}) + \alpha T(\vec{v}) &= T\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix} + \alpha \begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} = \begin{pmatrix} u_1 + \alpha v_1 + u_2 + \alpha v_2 \\ u_3 + \alpha v_3 \end{pmatrix} \end{align*} \end{split}\]

therefore \(T\) is a linear transformation.

(e) \(T\) is not a linear transformation since

\[\begin{split} \begin{align*} T\left( \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \end{pmatrix} \right) &= T \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 7 \\ 1 \end{pmatrix}, \\ T\begin{pmatrix} 1 \\ 0 \end{pmatrix} + T \begin{pmatrix} 1 \\ 1 \end{pmatrix} &= \begin{pmatrix} 4 \\ 0 \end{pmatrix} + \begin{pmatrix} 4 \\ 1 \end{pmatrix} = \begin{pmatrix} 8 \\ 1 \end{pmatrix}. \end{align*} \end{split}\]

(f) Let \(u = f(x), v = g(x) \in P(\mathbb{R})\) and \(\alpha \in \mathbb{R}\):

\[\begin{split} \begin{align*} T(u + \alpha v) &= T(f(x) + \alpha g(x)) = \frac{\mathrm{d}}{\mathrm{d} x}(f(x) + \alpha g(x)) = \frac{\mathrm{d}}{\mathrm{d} x}f(x) + \alpha \frac{\mathrm{d}}{\mathrm{d} x} g(x), \\ T(u) + \alpha T(v) &= T(f(x)) + \alpha T(g(x)) = \frac{\mathrm{d}}{\mathrm{d} x}f(x) + \alpha \frac{\mathrm{d}}{\mathrm{d} x}g(x), \end{align*} \end{split}\]

therefore \(T\) is a linear transformation.

(g) Let \(u = f(x), v = g(x) \in P(\mathbb{R})\) and \(\alpha \in \mathbb{R}\):

\[\begin{split} \begin{align*} T(u + \alpha v) &= T(f(x) + \alpha g(x)) = x(f(x) + \alpha g(x)) = xf(x) + \alpha x g(x), \\ T(u) + \alpha T(v) &= T(f(x)) + \alpha T(g(x)) = xf(x) + \alpha x g(x), \end{align*} \end{split}\]

therefore \(T\) is a linear transformation.

Solution to Exercise 6.2

The transformation matrix is

\[\begin{split} A = \begin{pmatrix} -1 & 3 \\ 1 & -4 \end{pmatrix} \end{split}\]

Calculating \(T \begin{pmatrix} 2 \\ 5 \end{pmatrix}\)

\[\begin{split} T \begin{pmatrix} 2 \\ 5 \end{pmatrix} = \begin{pmatrix} -1 & 3 \\ 1 & -4 \end{pmatrix} \begin{pmatrix} 2 \\ 5 \end{pmatrix} = \begin{pmatrix} 13 \\ -18 \end{pmatrix}, \end{split}\]

therefore \(T\begin{pmatrix} 2 \\ 5 \end{pmatrix} = \begin{pmatrix} 13 \\ -18 \end{pmatrix}\).

Solution to Exercise 6.3

The transformation matrix is

\[\begin{split} A = \begin{pmatrix} 1 & -2 \\ 2 & 3 \end{pmatrix}, \end{split}\]

so the inverse is

\[\begin{split} A^{-1} = \frac{1}{7} \begin{pmatrix} 3 & 2 \\ -2 & 1 \end{pmatrix}. \end{split}\]

Therefore

\[\begin{split} \vec{u} = A^{-1} \begin{pmatrix} -1 \\ 5 \end{pmatrix} = \frac{1}{7} \begin{pmatrix} 3 & 2 \\ -2 & 1 \end{pmatrix} \begin{pmatrix} -1 \\ 5 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \end{pmatrix}. \end{split}\]

Solution to Exercise 6.4

The transformation matrix is determined using equation (6.2) which is

\[A = \begin{pmatrix} T(\vec{u}_1) & T(\vec{u}_2) & \cdots & T(\vec{u}_n) \end{pmatrix} \begin{pmatrix} \vec{u}_1 & \vec{u}_2 & \cdots & \vec{u}_n \end{pmatrix}^{-1}.\]

Using Gauss-Jordan elimination to calculate the inverse of \((\vec{u}_1, \vec{u}_2, \vec{u}_3)^{-1}\)

\[\begin{split} \begin{align*} & \left( \begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ -1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 2 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{l} \\ R_2 + R_1 \\ \phantom{x} \end{array} \\ \\ \longrightarrow \qquad & \left( \begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 2 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{l} \\ \\ R_3 - 2 R_2 \end{array} \\ \\ \longrightarrow \qquad & \left( \begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & -2 & -2 & 1 \end{array} \right) \begin{array}{l} R_1 + R_3 \\ \phantom{x} \\ \phantom{x} \end{array} \\ \\ \longrightarrow \qquad & \left( \begin{array}{rrr|rrr} 1 & 0 & 0 & -1 & -2 & 1 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & -2 & -2 & 1 \end{array} \right) \end{align*} \end{split}\]

So \((\vec{u}_1, \vec{u}_2, \vec{u}_3)^{-1} = \begin{pmatrix} -1 & -2 & 1 \\ 1 & 1 & 0 \\ -2 & -2 & 1 \end{pmatrix}\) and

\[\begin{split} \begin{align*} A &= \begin{pmatrix} 1 & 6 & 2 \\ -2 & 5 & 4 \\ -4 & 10 & 7 \end{pmatrix} \begin{pmatrix} -1 & -2 & 1 \\ 1 & 1 & 0 \\ -2 & -2 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 3 \\ -1 & 1 & 2 \\ 0 & 4 & 3 \end{pmatrix}. \end{align*} \end{split}\]

Checking \(A\)

\[\begin{split} T \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 3 \\ -1 & 1 & 2 \\ 0 & 4 & 3 \end{pmatrix} \begin{pmatrix}1 \\ -1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ -2 \\ - 4 \end{pmatrix} \quad \checkmark \end{split}\]

Solution to Exercise 6.5

The transformation matrix is

\[\begin{split} \begin{align*} Rot\left(\pi/6\right) &= \begin{pmatrix} \cos(\pi/6) & -\sin(\pi/6) \\ \sin(\pi/6) & \cos(\pi/6) \end{pmatrix} \\ &= \begin{pmatrix} \sqrt{3}/2 & -1/2 \\ 1/2 & \sqrt{3}/2 \end{pmatrix} \end{align*} \end{split}\]

therefore

\[\begin{split} \begin{align*} Rot\left(\frac{\pi}{6}\right) \begin{pmatrix} 2 \\ 1 \end{pmatrix} &= \begin{pmatrix} \sqrt{3}/2 & -1/2 \\ 1/2 & \sqrt{3}/2 \end{pmatrix} \begin{pmatrix} 2 \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} \sqrt{3} - 1/2 \\ 1 + \sqrt{3}/2 \end{pmatrix} \approx \begin{pmatrix} 1.2321 \\ 1.8660 \end{pmatrix} \end{align*} \end{split}\]

Solution to Exercise 6.6

The transformation matrix is

\[\begin{split} Re\!f \left(\pi/3\right) = \begin{pmatrix} \cos(2\pi/3) & \sin(2\pi/3) \\ \sin(2\pi/3) & -\cos(2\pi/3) \end{pmatrix} \begin{pmatrix} -1/2 & \sqrt{3}/2 \\ \sqrt{3}/2 & 1/2 \end{pmatrix} \end{split}\]

therefore

\[\begin{split} \begin{align*} Re\!f \left(\pi/3\right) \begin{pmatrix} 5 \\ 3 \end{pmatrix} &= \begin{pmatrix} -1/2 & \sqrt{3}/2 \\ \sqrt{3}/2 & 1/2 \end{pmatrix} \begin{pmatrix} 5 \\ 3 \end{pmatrix} \\ &= \begin{pmatrix} 3\sqrt{3}/2 - 5/2 \\ 3/2 + 5\sqrt{3}/2 \end{pmatrix} \approx \begin{pmatrix} 0.0981 \\ 5.8301 \end{pmatrix}. \end{align*} \end{split}\]

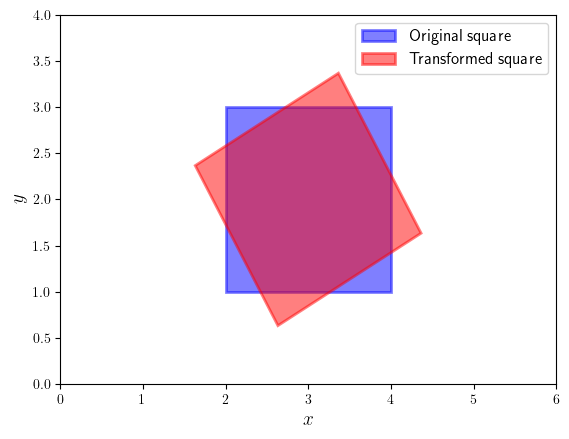
Solution to Exercise 6.7

(a) \(\begin{pmatrix} 2 & 4 & 4 & 2 \\ 1 & 1 & 3 & 3 \\ 1 & 1 & 1 & 1 \end{pmatrix} \)

(b) Translate by \((-3, -2)^\mathsf{T}\) so that the centre of the square is at the origin:

\[\begin{split} \begin{align*} T \begin{pmatrix} -3 \\ -2 \end{pmatrix} = \begin{pmatrix} 1 & 0 & -3 \\ 0 & 1 & -2 \\ 0 & 0 & 1 \end{pmatrix} \end{align*} \end{split}\]

Rotate by \(\pi/3\) clockwise about the origin:

\[\begin{split} \begin{align*} Rot\left(-\frac{\pi}{3}\right) &= \begin{pmatrix} \cos(\pi/3) & \sin(\pi/3) & 0 \\ -\sin(\pi/3) & \cos(\pi/3) & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} 1/2 & \sqrt{3}/2 & 0 \\ -\sqrt{3}/2 & 1/2 & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &\approx \begin{pmatrix} 0.5 & 0.8660 & 0 \\ -0.8660 & 0.5 & 0 \\ 0 & 0 & 1 \end{pmatrix} \end{align*} \end{split}\]

Translate by \((3, 2)^\mathsf{T}\) so that the centre of the square is back to \(\vec{c}\)

\[\begin{split} \begin{align*} T \begin{pmatrix} 3 \\ 2 \end{pmatrix} &= \begin{pmatrix} 1 & 0 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{pmatrix} \end{align*} \end{split}\]

(c) Calculate composite alignment matrix

\[\begin{split} \begin{align*} A &= T \begin{pmatrix} 3 \\ 2 \end{pmatrix} \cdot Rot\left(-\frac{\pi}{3}\right) \cdot T \begin{pmatrix} -3 \\ -2 \end{pmatrix} \\ &= \begin{pmatrix} 1 & 0 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1/2 & \sqrt{3}/2 & 0 \\ -\sqrt{3}/2 & 1/2 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & -3 \\ 0 & 1 & -2 \\ 0 & 0 & 1 \end{pmatrix} \\ &= \begin{pmatrix} 1/2 & \sqrt{3}/2 & 3/2 - \sqrt{3} \\ -\sqrt{3}/2 & 1/2 & 1 + 3\sqrt{3}/2 \\ 0 & 0 & 1 \end{pmatrix} \\ &\approx \begin{pmatrix} 0.5 & 0.8660 & -0.2321 \\ -0.8660 & 0.5 & 3.5981 \\ 0 & 0 & 1 \end{pmatrix}. \end{align*} \end{split}\]

Apply composite transformation matrix

\[\begin{split} \begin{align*} AP &= \begin{pmatrix} 1/2 & \sqrt{3}/2 & 3/2 - \sqrt{3} \\ -\sqrt{3}/2 & 1/2 & 1 + 3\sqrt{3}/2 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 2 & 4 & 4 & 2 \\ 1 & 1 & 3 & 3 \\ 1 & 1 & 1 & 1 \end{pmatrix} \\ &= \begin{pmatrix} 5/2 - \sqrt{3}/2 & 7/2 - \sqrt{3}/2 & \sqrt{3}/2 + 7/2 & \sqrt{3}/2 + 5/2 \\ \sqrt{3}/2 + 3/2 & 3/2 - \sqrt{3}/2 & 5/2 - \sqrt{3}/2 & \sqrt{3}/2 + 5/2 \\ 1 & 1 & 1 & 1 \end{pmatrix} \\ &\approx \begin{pmatrix} 1.634 & 2.634 & 4.366 & 3.366 \\ 2.366 & 0.634 & 1.634 & 3.366 \\ 1 & 1 & 1 & 1 \end{pmatrix} \end{align*} \end{split}\]