2.8. Consistent, inconsistent and indeterminate systems

So far all of the examples of solving systems of linear equations have had a single unique solution. This will not always be the case and it is important that we consider the different situations that can arise when dealing with systems of equations. A useful measure of a system that is used to determine the number of solutions to a system of linear equations is the rank of a matrix.

Definition 2.7 (Rank of a matrix)

The rank of a matrix \(A\) denoted by \(\operatorname{rank}(A)\) is the number of non-zero rows of the row echelon form of \(A\).

To compute the rank of a matrix we simply use elementary row operations to row reduce to row echelon form and count the number of non-zero rows.

Definition 2.8 (Consistent, inconsistent and indeterminate systems)

A system of equations is said to be consistent if it has a solution, otherwise it is said to be an inconsistent. If a system of equations has more than one solution then it is said to be indeterminate.

2.8.1. Consistent systems

We can visualise consistent systems by considering the plot of a system with two variables, \(x_1\) and \(x_2\). If the lines that represent each equation in a system intersect at a single point then the point of intersection is the solution to the system. Consider the following system of linear equations

\[\begin{split} \begin{align*} x_1 - x_2 &= 1, \\ x_1 + x_2 &= 3. \end{align*} \end{split}\]

The lines for these two equations have been plotted in Fig. 2.4 below.

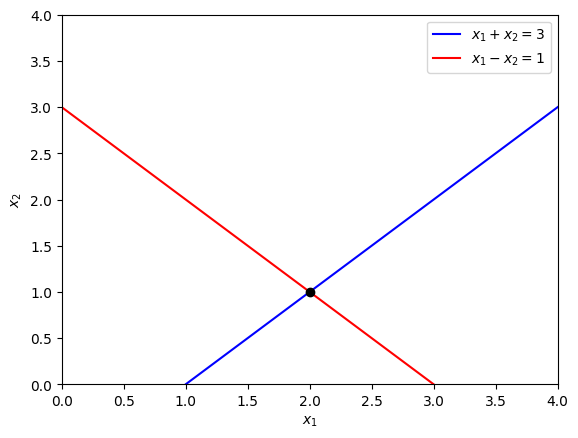
Fig. 2.4 Plots of the lines \(x_1 + x_2 = 3\) and \(x_1 - x_2 = 1\).

The two lines intersect at \((2,1)\) so this system is consistent and has a unique solution. This can easily be confirmed using Gaussian elimination.

\[\begin{split} \begin{align*} & \left( \begin{array}{cc|c} 1 & -1 & 1 \\ 1 & 1 & 3 \end{array} \right) \begin{array}{l} \\ R_2 - R_1 \end{array} \longrightarrow & \left( \begin{array}{cc|c} 1 & -1 & 1 \\ 0 & 2 & 2 \end{array} \right) \end{align*} \end{split}\]

Solving by back substitution gives \(x_1 = 2\) and \(x_2 = 1.\)

Theorem 2.5 (Consistent systems)

A system of linear equations \(A\vec{x} = \vec{b}\) is consistent if \(\operatorname{rank}(A) = \operatorname{rank}(A \mid \vec{b})\).

2.8.2. Inconsistent systems

If the lines that represent each equation in a system with two variables do not intersect then they must be parallel and we have an inconsistent system. Consider the following system of linear equations

\[\begin{split} \begin{align*} x_1 - x_2 &= 1, \\ x_1 - x_2 & = -1. \end{align*} \end{split}\]

The lines for these two equations have been plotted in Fig. 2.5 below.

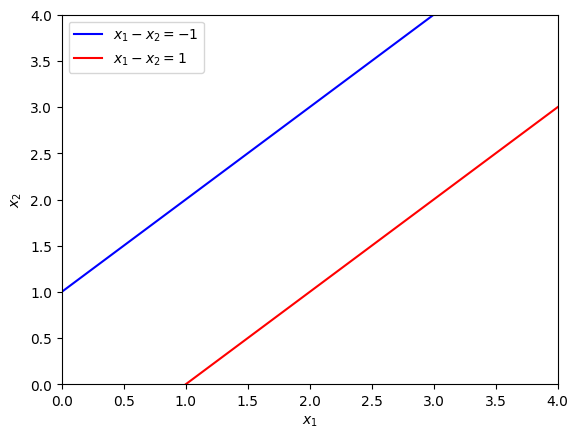
Fig. 2.5 Plots of the lines \(x_1 - x_2 = 1\) and \(x_1 - x_2 = -1\).

The two lines do not intersect so this system does not have a solution. If we attempt to solve this using Gaussian elimination

\[\begin{split} \begin{align*} & \left( \begin{array}{cc|c} 1 & -1 & 1 \\ 1 & -1 & -1 \end{array} \right) \begin{array}{l} \\ R_2 - R_1 \end{array} & \longrightarrow & \left( \begin{array}{cc|c} 1 & -1 & 1 \\ 0 & 0 & -2 \end{array} \right) \end{align*} \end{split}\]

so the second equation is \(0x_1 + 0x_2 = -2\) which is clearly impossible. This leads to the following theorem regarding inconsistent systems.

Theorem 2.6 (Inconsistent systems)

A system of linear equations is inconsistent if \(A\vec{x} = \vec{b}\) is inconsistent if \(\operatorname{rank}(A) < \operatorname{rank}(A \mid \vec{b})\).

2.8.3. Indeterminate systems

If the lines that represent each equation in a system with two variables are equivalent to each other then we have an indeterminate system where we have an infinite number of solutions. Consider the following system of linear equations

\[\begin{split} \begin{align*} x_1 - x_2 &= 1, \\ 2x_1 - 2x_2 &= 2. \end{align*} \end{split}\]

The lines for these two equations have been plotted in Fig. 2.6 below.

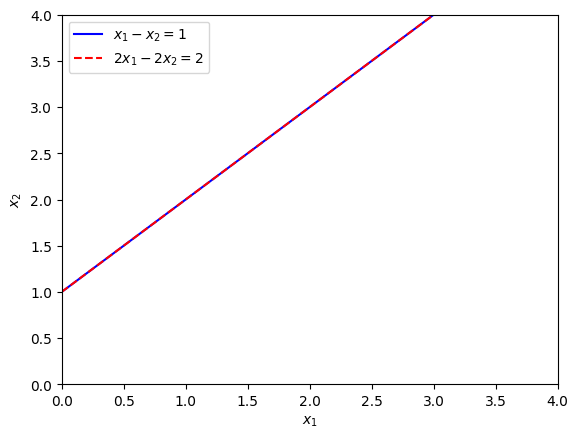
Fig. 2.6 Plots of the lines \(x_1 - x_2 = 1\) and \(2x_1 - 2x_2 = 2\).

The two lines are the same so any point along either line represents a solution to the system. If we attempt to solve this using Gaussian elimination

\[\begin{split} \begin{align*} \left( \begin{array}{cc|c} 1 & -1 & 1 \\ 2 & -2 & 2 \end{array} \right) \begin{array}{l} \\ R_2 - 2R_1 \end{array} \longrightarrow \quad \left( \begin{array}{cc|c} 1 & -1 & 1 \\ 0 & 0 & 0 \end{array} \right) \end{align*} \end{split}\]

so since the second equation has been eliminated we have a single equation \(x_1 - x_2 = 1\).

Theorem 2.7 (indeterminate systems)

A system of linear equations with \(n\) unknowns \(A\vec{x} = \vec{b}\) is indeterminate if \(\operatorname{rank}(A) < n\).

If we have an indeterminate system, the variables that correspond to columns in coefficient matrix without pivots (i.e., we cannot solve for these variables) are called free variables. We express the solution of indeterminate systems by assigning a parameter (\(r\), \(s\), \(t\) etc.) to the free variables and proceed is normal. For example, in our system \(x_2\) is a free variable so let \(x_2 = r\) where \(r \in \mathbb{R}\) and

\[ x_1 - r = 1, \]

so the solution is \(x_1 = 1 + r\) and \(x_2 = r\). Choosing any value of \(r\) gives a solution to the system. For example, if \(r=1\) then \(x_1 = 2\) and \(x_2 = 1\). Alternatively if \(r = -1\) then \(x_1 = 0\) and \(x_2 = -1\).

Example 2.7

Determine the rank of the coefficient matrix and the augmented matrix for the following systems of linear equations and classify them as either consistent, inconsistent or indeterminate systems.

(i)   \(\begin{array}{rl} 3x_1 + x_2 - 2x_3 \!\!\!\! &= 1, \\ x_1 - x_2 + 2x_3 \!\!\!\! &= 3, \\ 2x_1 - 3x_2 + 7x_3 \!\!\!\! &= 4. \end{array}\);

Solution

\[\begin{split} \begin{align*} & \left( \begin{array}{ccc|c} 3 & 1 & -2 & 1 \\ 1 & -1 & 2 & 3 \\ 2 & -3 & 7 & 4 \end{array} \right) \begin{array}{l} R_1 \leftrightarrow R_2 \\ \phantom{x} \\ \phantom{x} \end{array} & \longrightarrow & \left( \begin{array}{ccc|c} 1 & -1 & 2 & 3 \\ 3 & 1 & -2 & 1 \\ 2 & -3 & 7 & 4 \end{array} \right) \begin{array}{l} \\ R_2 - 3R_1 \\ R_3 - 2R_1 \end{array} \\ \\ \longrightarrow & \left( \begin{array}{ccc|c} 1 & -1 & 2 & 3 \\ 0 & 4 & -8 & -8 \\ 0 & -1 & 3 & -2 \end{array} \right) \begin{array}{l} \\ \\ R_3 + \frac{1}{4}R_2 \end{array} & \longrightarrow & \left( \begin{array}{ccc|c} 1 & -1 & 2 & 3 \\ 0 & 4 & -8 & -8 \\ 0 & 0 & 1 & -4 \end{array} \right) \end{align*} \end{split}\]

The augmented matrix is now in reduced row echelon form. Since \(\operatorname{rank}(A) = \operatorname{rank}(A \mid \vec{b}) = 3\) then this is a consistent system by the theorem for consistent systems. Using back substitution the solution is \(x_1 = 1\), \(x_2 = -10\) and \(x_3 = -4\).

(ii)   \(\begin{array}{rl} x_1 - x_2 + 2x_3 \!\!\!\! &= 3, \\ 2x_1 - 3x_2 + 7x_3 \!\!\!\! &= 4, \\ -x_1 + 3x_2 - 8x_3 \!\!\!\! &= 1. \end{array}\)

Solution

\[\begin{split} \begin{align*} & \left( \begin{array}{ccc|c} 1 & -1 & 2 & 3 \\ 2 & -3 & 7 & 4 \\ -1 & 3 & -8 & 1 \end{array} \right) \begin{array}{l} \\ R_2 - 2R_1 \\ R_3 + R_1 \end{array} & \longrightarrow & \left( \begin{array}{ccc|c} 1 & -1 & 2 & 3 \\ 0 & -1 & 3 & -2 \\ 0 & 2 & -6 & 4 \end{array} \right) \begin{array}{l} \\ \\ R_3 + 2R_2 \end{array} \\ \\ \longrightarrow & \left( \begin{array}{ccc|c} 1 & -1 & 2 & 3 \\ 0 & -1 & 3 & -2 \\ 0 & 0 & 0 & 0 \end{array} \right) \end{align*} \end{split}\]

The augmented matrix is now in reduced row echelon form. Since \(\operatorname{rank}(A) = \operatorname{rank}(A \mid \vec{b}) = 2\) then this is a consistent system by the theorem for consistent systems. Furthermore, since \(\operatorname{rank}(A) \) is less that the number of unknowns then this is an indeterminate system by the theorem for indeterminate systems. Let \(x_3 = r\) then using back substitution we have \(x_1 = 5 + r\) and \(x_2 = 2 + 3r\).

(iii)   \(\begin{array}{rcl} x_1 + x_2 - 2x_3 \!\!\!\! &= 1, \\ 2x_1 - x_2 + x_3 \!\!\!\! &= 9, \\ x_1 + 4x_2 - 7x_3 \!\!\!\! &= 2. \end{array}\)

Solution

\[\begin{split} \begin{align*} & \left( \begin{array}{ccc|c} 1 & 1 & -2 & 1 \\ 2 & -1 & 1 & 9 \\ 1 & 4 & -7 & 2 \end{array} \right) \begin{array}{l} \\ R_2 - 2R_1 \\ R_3 - R_1 \end{array} & \longrightarrow & \left( \begin{array}{ccc|c} 1 & 1 & -2 & 1 \\ 0 & -3 & 5 & 7 \\ 0 & 3 & -5 & 1 \end{array} \right) \begin{array}{l} \\ \\ R_3 + R_2 \end{array} \\ \\ \longrightarrow & \left( \begin{array}{ccc|c} 1 & 1 & -2 & 1 \\ 0 & -3 & 5 & 7 \\ 0 & 0 & 0 & 8 \end{array} \right) \end{align*} \end{split}\]

The augmented matrix is now in reduced row echelon form and \(\operatorname{rank}(A) = 2\) and \(\operatorname{rank}(A \mid \vec{b}) = 3\). Since \(\operatorname{rank}(A) < \operatorname{rank}(A \mid \vec{b})\) then this is an inconsistent system by the theorem for inconsistent systems and does not have a solution.