6G6Z3017 Computational Methods in ODEs
The general form of an explicit Runge-Kutta method for solving an Initial Value Problem (IVP) is
\[ \begin{align*} y_{n+1} &= y_n + h(b_1k_1 + b_2k_2 + \cdots + b_sk_s), \\ k_1 &= f(t_n, y_n), \\ k_2 &= f(t_n + c_2h, y_n + ha_{21}k_1), \\ k_3 &= f(t_n + c_3h, y_n + h(a_{31}k_1 + a_{32}k_2), \\ &\vdots \\ k_s &= f(t_n + c_sh, y_n + h(a_{s1}k_1 + a_{s2}k_2 + \cdots + a_{s,s-1}k_{s-1}). \end{align*} \]
To apply an explicit Runge-Kutta method we calculate the stage values \(k_1, k_2, \dots, k_s\) using the known values of \(t_n\) and \(y_n\) and the step length \(h\). Then the solution over one step \(y_{n+1}\) is then calculated using the values of \(k_1, k_2, \ldots, k_s\).
Note
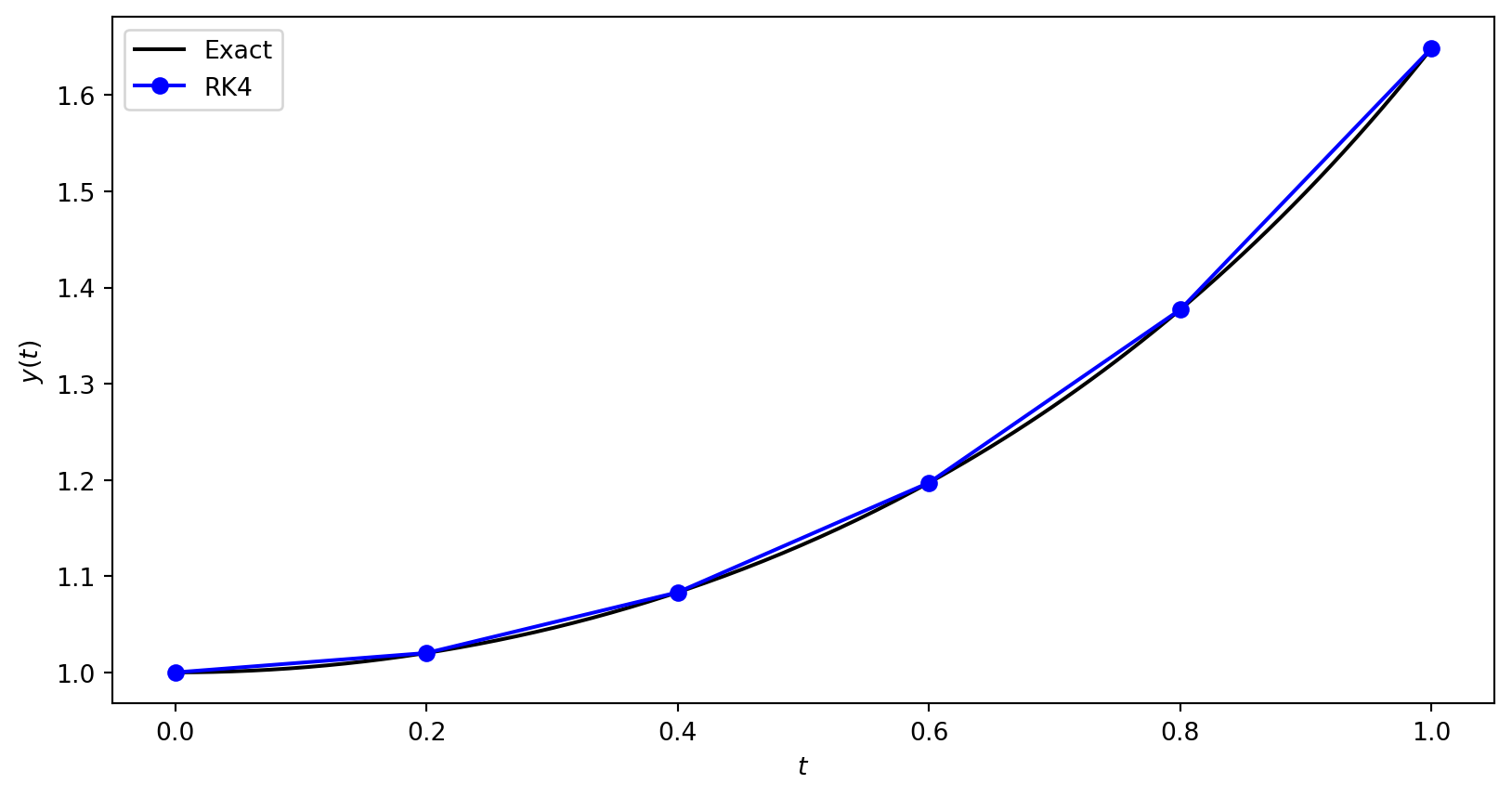
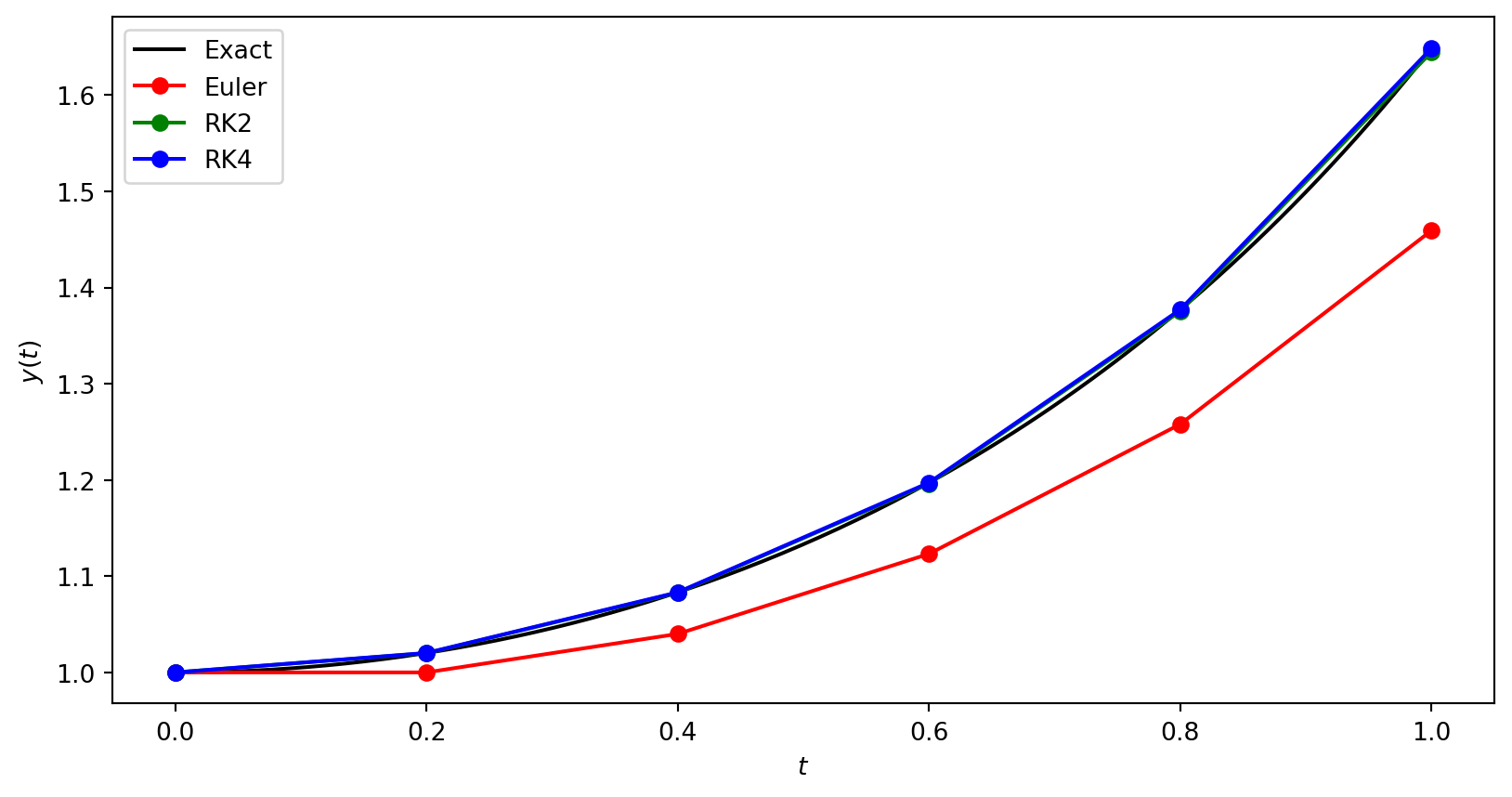
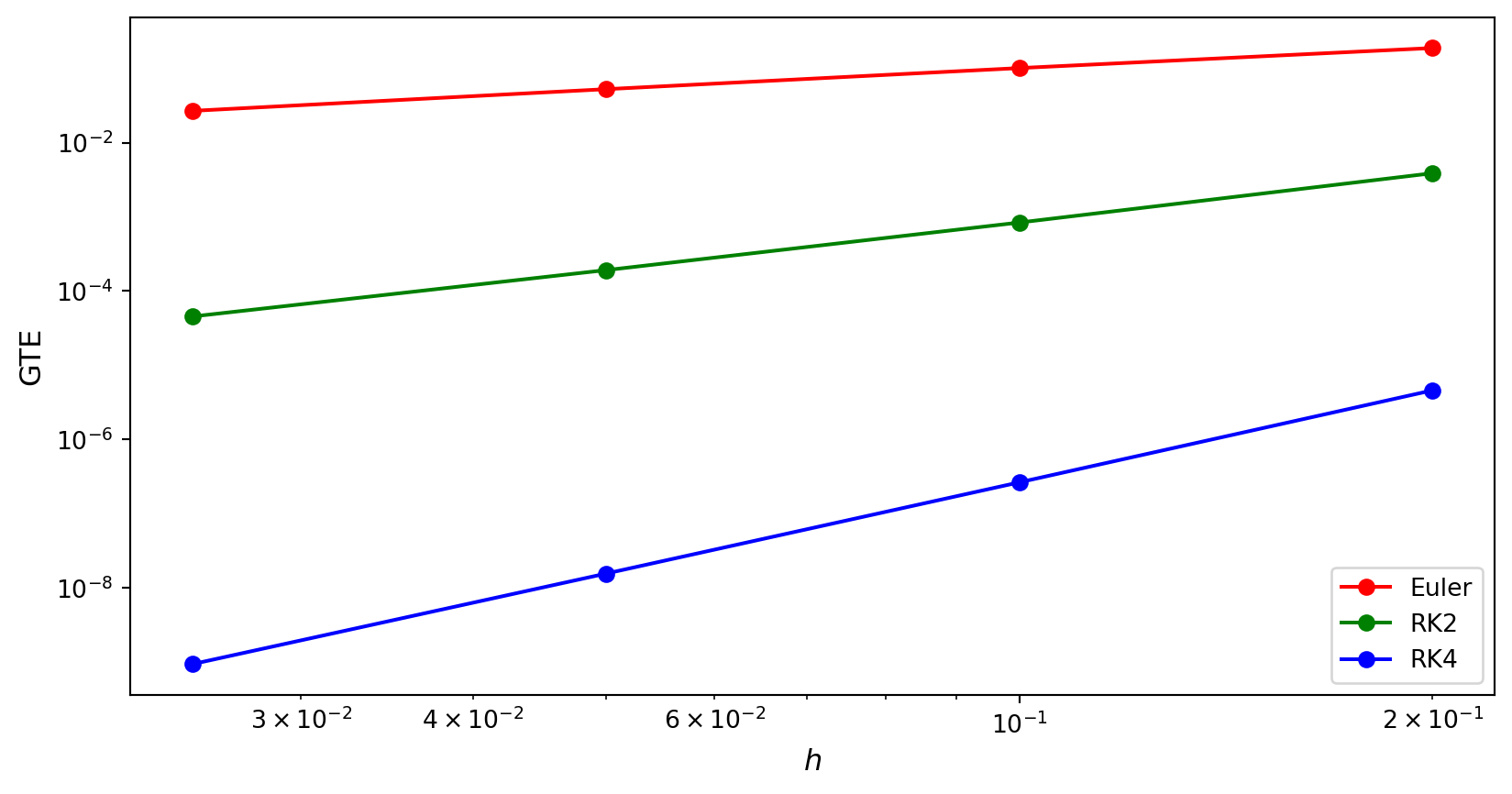
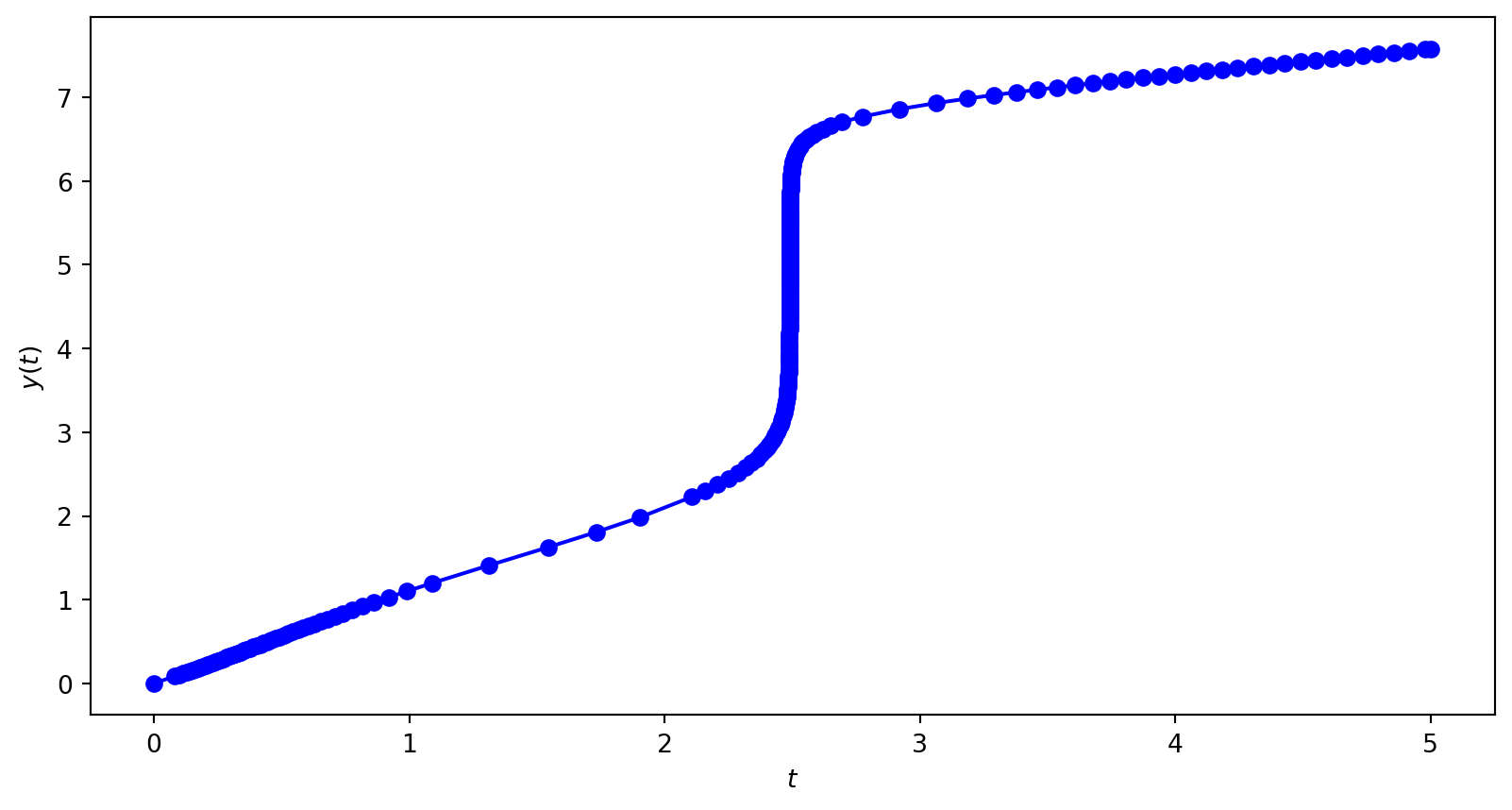
Inputs A first-order ODE of the form \(y' = f(t, y)\), a domain \(t \in [t_0, t_{\max}]\), an initial value \(y(t_0) = y_0\) and a step length \(h\)
Outputs \((t_0, t_1, \ldots)\) and \((y_0, y_1, \ldots)\)
The RK4 method is
\[\begin{align*} \begin{array}{c|cccc} 0 & 0 \\ \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & 0 & \frac{1}{2} \\ 1 & 0 & 0 & 1 \\ \hline & \frac{1}{6} & \frac{1}{3} & \frac{1}{3} & \frac{1}{6} \end{array} \end{align*}\]
Calculate the solution to the following initial value problem using the RK4 method with \(h = 0.2\)
\[\begin{align*} y'=ty, \qquad t\in [0,1], \qquad y(0)=1. \end{align*}\]
Calculate the number of steps required
\[nsteps = \left\lfloor \frac{t_{\max} - t_0}{h} \right\rfloor = \left\lfloor \frac{1 - 0}{0.2} \right\rfloor = 5.\]
Calculating the stage values for the first step
\[ \begin{align*} k_1 &= f(t_0, y_0) = t_0 y_0 \\ &= (0)(1) = 0, \\ k_2 &= f(t_0 + \tfrac{1}{2}h, y_0 + \tfrac{1}{2}hk_1) = (t_0 + \tfrac{1}{2}h)(y_0 + \tfrac{1}{2}hk_1) \\ &= (0 + \tfrac{1}{2}(0.2))(1 + \tfrac{1}{2}(0.2)(0)) = 0.1, \\ k_3 &= f(t_0 + \tfrac{1}{2}h, y_0 + \tfrac{1}{2}hk_2) = (t_0 + \tfrac{1}{2}h)(y_0 + \tfrac{1}{2}hk_2) \\ &= (0 + \tfrac{1}{2}(0.2))(1 + \tfrac{1}{2}(0.2)(0.1)) = 0.101, \\ k_4 &= f(t_0 + h, y_0 + hk_2) = (t_0 + h)(y_0 + hk_2) \\ &= (0 + 0.2)(1 + 0.2(0.1)) = 0.204. \end{align*} \]
The solution at the first step is
\[ \begin{align*} y_1 &= y_0 + \frac{h}{6}(k_1 + 2k_2 + 2k_3 + k_4) \\ &= 1 + \frac{0.2}{6}(0 + 2(0.1) + 2(0.101) + 0.204040) = 1.020201, \\ t_1 &= t_0 + h = 0 + 0.2 = 0.2, \end{align*} \]
Repeating this for the other steps in the method gives the values in the table below.
| \(n\) | \(t_n\) | \(y_n\) | \(k_1\) | \(k_2\) | \(k_3\) | \(k_4\) |
|---|---|---|---|---|---|---|
| 0 | 0.0 | 1.000000 | - | - | - | - |
| 1 | 0.2 | 1.020201 | 0.000000 | 0.100000 | 0.101000 | 0.204040 |
| 2 | 0.4 | 1.083287 | 0.204040 | 0.312182 | 0.315426 | 0.433315 |
| 3 | 0.6 | 1.197217 | 0.433315 | 0.563309 | 0.569809 | 0.718349 |
| 4 | 0.8 | 1.377126 | 0.718330 | 0.888335 | 0.900235 | 1.101811 |
| 5 | 1.0 | 1.648717 | 1.101701 | 1.338567 | 1.359885 | 1.649103 |
def rk4(f, tspan, y0, h):
nsteps = int((tspan[1] - tspan[0]) / h)
m = len(y0)
t = np.zeros(nsteps + 1)
y = np.zeros((nsteps + 1, m))
t[0] = tspan[0]
y[0,:] = y0
for n in range(nsteps):
k1 = f(t[n], y[n,:])
k2 = f(t[n] + 0.5 * h, y[n,:] + 0.5 * h * k1)
k3 = f(t[n] + 0.5 * h, y[n,:] + 0.5 * h * k2)
k4 = f(t[n] + h, y[n,:] + h * k3)
y[n+1,:] = y[n,:] + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4);
t[n+1] = t[n] + h
return t, yfunction [t, y] = rk4(f, tspan, y0, h)
nsteps = floor((tspan(2) - tspan(1)) / h);
m = length(y0);
t = zeros(1, nsteps + 1);
y = zeros(nsteps + 1, m);
t(1) = tspan(1);
y(1,:) = y0;
for n = 1 : length(t) - 1
k1 = f(t(n), y(n,:));
k2 = f(t(n) + 1/2 * h, y(n,:) + 1/2 * h * k1);
k3 = f(t(n) + 1/2 * h, y(n,:) + 1/2 * h * k2);
k4 = f(t(n) + h, y(n,:) + h * k3);
y(n+1,:) = y(n,:) + h / 6 * (k1 + 2 * k2 + 2 * k3 + k4);
t(n+1) = t(n) + h;
end
y = y;
end| t | y | Exact |
|:----:|:---------:|:---------:|
| 0.00 | 1.000000 | 1.000000 |
| 0.20 | 1.020201 | 1.020201 |
| 0.40 | 1.083287 | 1.083287 |
| 0.60 | 1.197217 | 1.197217 |
| 0.80 | 1.377126 | 1.377128 |
| 1.00 | 1.648717 | 1.648721 |
The three methods have been applied using step lengths \(h = 0.2, 0.1, 0.05, 0.025\) and the global truncation errors at \(t = 1\) are tabulated below.
| \(h\) | Euler | RK2 | RK4 |
|---|---|---|---|
| 0.200 | 1.89e-01 | 3.88e-03 | 4.59e-06 |
| 0.100 | 1.02e-01 | 8.40e-04 | 2.64e-07 |
| 0.050 | 5.28e-02 | 1.92e-04 | 1.55e-08 |
| 0.025 | 2.69e-02 | 4.55e-05 | 9.33e-10 |
The order of the methods \(n\) can be approximated using \(n \approx \dfrac{\log(E_n(h_1)) - \log(E_n(h_2))}{\log(h_1) - \log(h_2)},\) for example, for the RK4 method
\[ \begin{align*} n & \approx \frac{\log(4.59 \times 10^{-6}) - \log(9.33 \times 10^{-10})}{\log(0.2) - \log(0.025)} = 4.09 \approx 4, \end{align*} \]
Using a fixed step length does not allow the method to take advantage of increasing the step length where the behaviour of the solution allows.
Adaptive step size control is a method that attempts to control the value of the step length based on accuracy requirements
So the step length \(h\) adjusts depending on the behaviour of the solution
Consider the case where we are applying a population model where the solution values are expected to be large. Let \(y^{(p)} = 1000000\) and \(y^{(p+1)} = 1000100\) be the order \(p\) and \(p+1\) solution then
\[ \textsf{absolute difference} = | y^{(p+1)} - y^{(p)} | = | 1000100 - 1000000 | = 100. \]
So if \(tol = 10^{-3}\) the step would consider to have failed and we would repeat the step. However,
\[ \textsf{relative difference} = \frac{|y^{(p+1)} - y^{(p)}|}{|y^{(p)}|} = \frac{|1000100 - 1000000|}{|1000000|} = 10^{-4}, \]
which is less than \(10^{-3}\) and the step would consider to be successful.
Now consider a case where we are applying a chemical kinetics model where the solution values are expected to be very small. If \(y^{(p)} = 1 \times 10^{-6}\) and \(y^{(p+1)} = 2\times 10^{-6}\) then
\[ \textsf{relative difference} = \frac{| y^{(p+1)} - y^{(p)} |}{|y^{(p)}|} = \frac{| 2\times 10^{-6} - 1 \times 10^{-6} |}{|1 \times 10^{-6}|} = 1, \]
which is greater than the accuracy tolerance of \(10^{-3}\) and the step would consider to have failed. However,
\[ \textsf{absolute difference} = | y^{(p+1)} - y^{(p)} | = | 2\times 10^{-6} - 1 \times 10^{-6} | = 10^{-6}, \]
which is a lot less than the accuracy tolerance and the step would consider to be successful.
We want an algorithm that can deal with both cases, so we use two accuracy tolerances, \(atol\) and \(rtol\) for the absolute and relative differences such that \(atol < rtol\), and a step is considered to have been successful if
\[ |y^{(p+1)} - y^{(p)}| < atol + rtol \cdot |y^{(p+1)}|. \]
Using \(atol = 10^{-6}\) and \(rtol = 10^{-3}\) for the population model example we have
\[ atol + rtol \cdot |y^{(p+1)}| = 10^{-6} + 10^{-3} \cdot |1000100| = 1000.100001. \]
Since \(|y^{(p+1)} - y^{(p)}| = 100 < 1000.100001\) the step is considered to be successful. Alternatively, for the chemical kinetics example we have
\[ atol + rtol \cdot |y^{(p+1)}| = 10^{-6} + 10^{-3} \cdot |2\times 10^{-6}| = 1.002\times 10^{-6}, \]
and since \(|y^{(p+1)} - y^{(p)}| = 10^{-6} < 1.002\times 10^{-6}\) the step is considered to be successful.
Let \(y^{(p)}\) and \(y^{(p+1)}\) denote the numerical solutions and \(y\) denote the exact solution then
\[ \begin{align*} y &= y^{(p)} + O(h^{p+1}), \\ y &= y^{(p+1)} + O(h^{p+2}). \end{align*} \]
Subtracting the second equation from the first gives
\[ \begin{align*} 0 &= y^{(p)} - y^{(p+1)} + O(h^{p+1}) + O(h^{p+2}) \\ |y^{(p+1)} - y^{(p)}| &= O(h^{p+1}) + O(h^{p+2}). \end{align*} \]
Let \(\Delta = |y^{(p)} - y^{(p+1)}|\) and since \(O(h^{p+1}) + O(h^{p+2}) = O(h^{p+1})\) then by the definition of \(O(h^n)\)
\[ \Delta = Ch^{p+1}. \]
We want to calculate a new step length \(h_{new}\) which results in a desired accuracy tolerance \(tol\), i.e.,
\[ tol = Ch_{new}^{p+1}.\]
Defining a ratio \(r\) between the new step length and current step length, \(r = h_{new} / h\), then
\[ \begin{align*} \frac{Ch_{new}^{p+1}}{Ch^{p+1}} &= \frac{tol}{\Delta} \\ r^{p+1} &= \frac{tol}{\Delta} \\ r &= \left( \frac{tol}{\Delta} \right)^{\frac{1}{p+1}}. \end{align*} \]
So when \(\Delta > tol\), \(r < 1\) and the step length is decreased, and when \(\Delta < tol\), \(r > 1\) and the step length is increased.
To prevent the step length being decreased too much we limit the value of \(r\) so that \(h\) is not increased or decreased too much
\[ h = h \max\left(0.1, 0.8 \left( \frac{tol}{\Delta} \right)^{\frac{1}{p+1}} \right). \]
We can use the value of \(rtol\) to give us an approximation for the initial value of \(h\)
\[ h = 0.8 \cdot rtol ^ {^\frac{1}{p+1}}. \]
Embedded Runge-Kutta methods are were the \(p\) and \(p+1\) solution share the same stage values \(k_i\) but uses a difference weighted sum of \(k_i\) to calculate \(y_{n+1}\)
The Butcher tableau for an embedded Runge-Kutta method takes the form
\[ \begin{align*} \begin{array}{c|ccccc} 0 & 0 \\ c_2 & a_{21} \\ c_3 & a_{31} & a_{32} \\ \vdots & \vdots & \vdots & \ddots \\ c_s & a_{s1} & a_{s2} & \cdots & a_{s,s-1} \\ \hline & b_1 & b_2 & \cdots & b_{s-1} & b_s \\ & b_1^* & b_2^* & \cdots & b_{s-1}^* & b_s^* \end{array} \end{align*} \]
Where the weights \(b_i\) and \(b_i^*\) that give an order \(p+1\) and \(p\) method respectively, i.e.,
\[ \begin{align*} y_{n+1}^{(p+1)} &= y_n + h (b_1 k_1 + b_2 k_2 + \cdots + b_s k_s), \\ y_{n+1}^{(p)} &= y_n + h (b_1^* k_1 + b_2^* k_2 + \cdots + b_s^* k_s), \end{align*} \]
Note
Bogacki-Shampine 3(2) Runge-Kutta method (RK23)
\[ \begin{align*} \begin{array}{c|cccc} 0 & \\ \frac{1}{2} & \frac{1}{2} \\ \frac{3}{4} & 0 & \frac{3}{4} \\ 1 & \frac{2}{9} & \frac{1}{3} & \frac{4}{9} \\ \hline & \frac{2}{9} & \frac{1}{3} & \frac{4}{9} & 0 \\ & \frac{7}{24} & \frac{1}{4} & \frac{1}{3} & \frac{1}{8} \end{array} \end{align*} \]
Note
Fehlberg’s order 5(4) Runge-Kutta method (RKF45)
\[ \begin{array}{c|cccccc} 0 & 0 \\ \frac{1}{4} & \frac{1}{4} \\ \frac{3}{8} & \frac{3}{32} & \frac{9}{32} \\ \frac{12}{13} & \frac{1932}{2197} & -\frac{7200}{2197} & \frac{7296}{2197} \\ 1 & \frac{439}{216} & -8 & \frac{3680}{513} & -\frac{845}{4104} \\ \frac{1}{2} & -\frac{8}{27} & 2 & -\frac{3544}{2565} & \frac{1859}{4104} & -\frac{11}{40} \\ \hline & \frac{16}{135} & 0 & \frac{6656}{12825} & \frac{28561}{56430} & -\frac{9}{50} & \frac{2}{55} \\ & \frac{25}{216} & 0 & \frac{1408}{2565} & \frac{2197}{4104} & -\frac{1}{5} & 0 \end{array} \]
Note
Use Bogacki-Shampine method to solve the following IVP using accuracy tolerances of \(atol = 10^{-6}\) and \(rtol = 10^{-3}\)
\[ y' = e^{t - y \sin(y)}, \qquad t \in [0, 5], \qquad y(0) = 0.\]
Here \(f(t, y) = e^{t - y\sin(y)}\), \(t= 0\) and \(y_0 = 0\). Calculating the initial step length gives
\[ h = 0.8 (rtol)^{^\frac{1}{3}} = 0.8(10^{-3})^{^\frac{1}{3}} = 0.8.\]
Calculating the first step of the Bogacki-Shampine 3(2) method gives
\[ \begin{align*} y^{(3)} &= 0.083096, & y^{(2)} &= 0.083081. \end{align*} \]
Calculate \(\Delta\) and \(tol\)
\[ \begin{align*} \Delta &= \| y^{(3)} - y^{(2)} \| = 0.083096 - 0.083081 = 1.563 \times 10^{-5}, \\ tol &= atol + rtol \cdot \|y^{(3)}\| = 10^{-6} + 10^{-3}(0.083096) = 8.410 \times 10^{-5}, \end{align*} \]
So \(\Delta < tol\) and the step has been successful.
Calculating the new value of \(h\)
\[ \begin{align*} h = h \max \left( 0.1, 0.8 \left( \frac{tol}{\Delta} \right)^{^\frac{1}{3}} \right) = 0.8 \max \left(0.1, 0.8 \left( \frac{8.410 \times 10^{-5}}{1.563 \times 10^{-5}} \right)^{^\frac{1}{3}} \right) = 0.112145. \end{align*} \]
The solution over the range \(t \in [0,1]\) is
Plot of the values of the step length \(h\) across the \(t\) domain
\(\max(h) = 0.232779\), \(\min(h) = 2.48 \times 10^{-05}\)
def rk23(f, tspan, y0, atol=1e-6, rtol=1e-3):
m = len(y0)
t = np.zeros(100000)
y = np.zeros((100000, m))
t[0] = tspan[0]
y[0,:] = y0
h = 0.8 * rtol ** (1 / 3)
n = 0
while t[n] < tspan[-1]:
k1 = f(t[0], y[0,:])
k2 = f(t[n] + 1/2 * h, y[n,:] + 1/2 * h * k1)
k3 = f(t[n] + 3/4 * h, y[n,:] + 3/4 * h * k2)
k4 = f(t[n] + h, y[n,:] + h * (2/9 * k1 + 1/3 * k2 + 4/9 * k3))
y3 = y[n,:] + h * (2/9 * k1 + 1/3 * k2 + 4/9 * k3)
y2 = y[n,:] + h * (7/24 * k1 + 1/4 * k2 + 1/3 * k3 + 1/8 * k4)
delta = np.linalg.norm(y3 - y2)
tol = atol + rtol * np.min(np.abs(y3))
if delta < tol:
y[n+1,:] = y3
t[n+1] = t[n] + h
n += 1
h = min(h * max(0.1, 0.8 * (tol / delta) ** (1/3), tspan[-1] - t[n]))
return t[:n+1], y[:n+1,:]function [t, y] = rk23(f, tspan, y0, atol, rtol)
m = length(y0);
t = zeros(100000, 1);
y = zeros(100000, m);
t(1) = tspan(1);
y(1,:) = y0;
h = 0.8 * rtol ^ (1/3);
n = 1;
while t(n) < tspan(2)
k1 = f(t(n), y(n,:));
k2 = f(t(n) + 1/2 * h, y(n,:) + 1/2 * h * k1);
k3 = f(t(n) + 3/4 * h, y(n,:) + 3/4 * h * k2);
k4 = f(t(n) + h, y(n,:) + h * (2/9 * k1 + 1/3 * k2 + 4/9 * k3));
y3 = y(n,:) + h * (2/9 * k1 + 1/3 * k2 + 4/9 * k3);
y2 = y(n,:) + h * (7/24 * k1 + 1/4 * k2 + 1/3 * k3 + 1/8 * k4);
delta = norm(y3 - y2);
tol = atol + rtol * min(abs(y3));
if delta < tol
y(n+1,:) = y3;
t(n+1) = t(n) + h;
n = n + 1;
end
h = min(h * max(0.1, 0.8 * (tol / delta) ^ (1/3)), tspan(2) - t(n));
end
t(n+1:end) = [];
y(n+1:end,:) = [];
end